
ЁОЬтФПЁПШчЭМЃЌЁЯACLЃН90ЁуЃЌACЃН4ЃЌЖЏЕуBдкЩфЯпCLЃЌCHЁЭABгкЕуHЃЌвдHЮЊдВаФЃЌHBЮЊАыОЖзїдВНЛЩфЯпBAгкЕуDЃЌНЛжБЯпCDгкЕуFЃЌНЛжБЯпBCгкЕуEЃЎЩшBCЃНmЃЎ

ЃЈ1ЃЉЕБЁЯAЃН30ЁуЪБЃЌЧѓЁЯCDBЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЕБmЃН2ЪБЃЌЧѓBEЕФГЄЖШЃЛ
ЃЈ3ЃЉдкЕуBЕФећИідЫЖЏЙ§ГЬжаЃЌ
ЂйЕБBCЃН3CEЪБЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФmЕФжЕЃЎ
ЂкСЌНгEHЃЌFHЃЌЕБtanЁЯFHEЃН![]() ЪБЃЌжБНгаДГіЁїFHDгыЁїEFHУцЛ§БШЃЎ
ЪБЃЌжБНгаДГіЁїFHDгыЁїEFHУцЛ§БШЃЎ
ЁОД№АИЁПЃЈ1ЃЉ60ЁуЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂйmЃН2
ЃЛЃЈ3ЃЉЂйmЃН2![]() Лђ4
Лђ4![]() ЃЛЂк
ЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтгЩHBЃНHDЃЌCHЁЭBDПЩжЊЃКCHЪЧBDЕФжаДЙЯпЃЌдйгЩЁЯAЃН30ЁуЕУЃКЁЯCDBЃНЁЯABCЃН60ЁуЃЛ
ЃЈ2ЃЉгЩЬтвтПЩжЊЕБmЃН2ЪБЃЌгЩЙДЙЩЖЈРэПЩЕУЃКABЃН2![]() ЃЌcosЁЯABCЃН
ЃЌcosЁЯABCЃН![]() ЃЌЙ§ЕуHзїHKЁЭBCгкЕуKЃЌРћгУДЙОЖЖЈРэПЩЕУНсТлЃЛ
ЃЌЙ§ЕуHзїHKЁЭBCгкЕуKЃЌРћгУДЙОЖЖЈРэПЩЕУНсТлЃЛ
ЃЈ3ЃЉЃЉЂйвЊЗжСНжжЧщПіЃКIЃЎЕБЕуEдкCгвВрЪБЃЌIIЃЎЕБЕуEдкCзѓВрЪБЃЛИљОнЯрЫЦШ§НЧаЮаджЪКЭЙДЙЩЖЈРэМДПЩЧѓЕУНсТлЃЛ
ЂкИљОнЬтвтЯШжЄУїEFЁЮBDЃЌИљОнЦНааЯпМфОрРыЯрЕШПЩЕУЃКЁїFHDгыЁїEFHИпЯрЕШЃЌУцЛ§БШЕШгкЕзжЎБШЃЌдйгЩtanЁЯFHEЃН![]() ПЩЧѓЕУ
ПЩЧѓЕУ![]() ЕФжЕМДПЩЃЎ
ЕФжЕМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпЁЯAЃН30ЁуЃЌЁЯACBЃН90ЁуЃЌ
ЁрЁЯABCЃН60ЁуЃЌ
ЁпHBЃНHDЃЌCHЁЭBDЃЌ
ЁрCHЪЧBDЕФжаДЙЯпЃЌ
ЁрCBЃНCDЃЌ
ЁрЁЯCDBЃНЁЯABCЃН60ЁуЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуHзїHKЁЭBCгкЕуKЃЌ

ЕБmЃН2ЪБЃЌBCЃН2ЃЌ
ЁрABЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрcosЁЯABCЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрBHЃНBCcosЁЯABCЃН![]() ЃЌ
ЃЌ
ЁрBKЃНBHcosЁЯABCЃН![]() ЃЌ
ЃЌ
ЁрBEЃН2BKЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйЗжСНжжЧщПіЃК
IЃЎЕБЕуEдкCгвВрЪБЃЌШчЭМ2ЃЌСЌНсDEЃЌгЩBDЪЧжБОЖЃЌЕУDEЁЭBCЃЌ

ЁпBCЃН3CEЃНmЃЌ
ЁрCEЃН![]() mЃЌBEЃН
mЃЌBEЃН![]() mЃЌ
mЃЌ
ЁпDEЁЮACЃЌ
ЁрЁїDEBЁЋЁїACBЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDEЃН![]() ACЃН
ACЃН![]() ЃЌ
ЃЌ
ЁпCDЃНCBЃНmЃЌ
ЁрRtЁїCDEжаЃЌгЩЙДЙЩЖЈРэЕУЃК ЃНm2ЃЌ
ЃНm2ЃЌ
ЁпmЃО0ЃЌ
ЁрmЃН2![]() ЃЛ
ЃЛ
IIЃЎЕБЕуEдкCзѓВрЪБЃЌШчЭМ3ЃЌСЌНсDEЃЌгЩBDЪЧжБОЖЃЌЕУDEЁЭBCЃЌ

ЁпBCЃН3CEЃЌ
ЁрCEЃН![]() mЃЌBEЃН
mЃЌBEЃН![]() mЃЌ
mЃЌ
ЁпDEЁЮACЃЌ
ЁрЁїDEBЁЋЁїACBЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDEЃН![]() ACЃН6ЃЌ
ACЃН6ЃЌ
ЁпCDЃНCBЃНmЃЌ
ЁрRtЁїCDEжаЃЌгЩЙДЙЩЖЈРэЕУЃК62+ ЃНm2ЃЌ
ЃНm2ЃЌ
ЁпmЃО0ЃЌ
ЁрmЃН4![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌЂйЕБBCЃН3CEЪБЃЌmЃН2![]() Лђ4
Лђ4![]() ЃЎ
ЃЎ
ЂкШчЭМ4ЃЌЙ§FзїFGЁЭHEгкЕуGЃЌ

ЁпCHЁЭABЃЌHBЃНHDЃЌ
ЁрCBЃНCDЃЌ
ЁрЁЯCBDЃНЁЯCDBЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрEFЁЮBDЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпдкRtЁїFHGжаЃЌ![]() ЃНtanЁЯFHEЃН
ЃНtanЁЯFHEЃН![]() ЃЌ
ЃЌ
ЩшFGЃН5kЃЌHGЃН12kЃЌдђFHЃН![]() ЃН
ЃН![]() ЃН13kЃЌ
ЃН13kЃЌ
ЁрDHЃНHEЃНFHЃН13kЃЌEGЃНHEЉHGЃН13kЉ12kЃНkЃЌ
ЁрEFЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() kЃЌ
kЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЯТСаЭјИёгЩаЁе§ЗНаЮзщГЩЃЌЕу![]() ЖМдке§ЗНаЮЭјИёЕФИёЕуЩЯ.
ЖМдке§ЗНаЮЭјИёЕФИёЕуЩЯ.
ЃЈ1ЃЉдкЭМ1жаЛГівЛИівдЯпЖЮ![]() ЮЊБпЃЌЧвгы
ЮЊБпЃЌЧвгы![]() УцЛ§ЯрЕШЕЋВЛШЋЕШЕФИёЕуШ§НЧаЮЃЛ
УцЛ§ЯрЕШЕЋВЛШЋЕШЕФИёЕуШ§НЧаЮЃЛ
ЃЈ2ЃЉдкЭМ2КЭЭМ3жаЗжБ№ЛГівЛИівдЯпЖЮ![]() ЮЊБпЃЌЧвгы
ЮЊБпЃЌЧвгы![]() ЯрЫЦЃЈЕЋВЛШЋЕШЃЉЕФИёЕуШ§НЧаЮЃЌВЂаДГіЫљЛШ§НЧаЮгы
ЯрЫЦЃЈЕЋВЛШЋЕШЃЉЕФИёЕуШ§НЧаЮЃЌВЂаДГіЫљЛШ§НЧаЮгы![]() ЕФЯрЫЦБШ.ЃЈЯрЭЌЕФЯрЫЦБШЫувЛжжЃЉ
ЕФЯрЫЦБШ.ЃЈЯрЭЌЕФЯрЫЦБШЫувЛжжЃЉ
ЃЈ1ЃЉ
ЃЈ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЕФзјБъЪЧЃЈ4ЃЌ0ЃЉЃЌВЂЧвOA=OC=4OBЃЌЖЏЕуPдкЙ§AЃЌBЃЌCШ§ЕуЕФХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкACЩЯЗНЕФХзЮяЯпЩЯгавЛЖЏЕуGЃЌШчЭМЃЌЕБЕуGдЫЖЏЕНФГЮЛжУЪБЃЌвдAGЃЌAOЮЊСкБпЕФЦНааЫФБпаЮЕкЫФИіЖЅЕуЧЁКУвВдкХзЮяЯпЩЯЃЌЧѓГіДЫЪБЕуGЕФзјБъЃЛ
ЃЈ3ЃЉШєХзЮяЯпЩЯДцдкЕуPЃЌЪЙЕУЁїACPЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЁбOЕФФкНгШ§НЧаЮЃЌABЪЧЁбOЕФжБОЖЃЌOFЁЭABЃЌНЛACгкЕуFЃЌЕуEдкABЕФбгГЄЯпЩЯЃЌЩфЯпEMОЙ§ЕуCЃЌЧвЁЯACE+ЁЯAFO=180Ёу.
ЃЈ1ЃЉЧѓжЄЃКEMЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯA=ЁЯE,BC=![]() ЃЌЧѓвѕгАВПЗжЕФУцЛ§.ЃЈНсЙћБЃСє
ЃЌЧѓвѕгАВПЗжЕФУцЛ§.ЃЈНсЙћБЃСє![]() КЭИљКХЃЉ.
КЭИљКХЃЉ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЙизЂбЇЩњГіааАВШЋЃЌЕїВщСЫФГАрбЇЩњГіааЗНЪНЃЌЕїВщНсЙћЗжЮЊЫФРрЃКAЉЦяздааГЕЃЌBЉВНааЃЌCЉзјЩчЧјАЭЪПЃЌDЉЦфЫќЃЌВЂНЋЕїЫНсЙћЛцжЦГЩвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
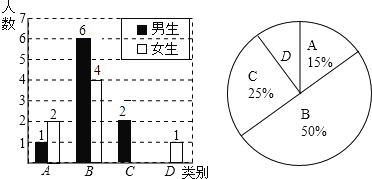
ЧыФуИљОнЭГМЦЭМЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮвЛЙВЕїЫСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉCРрХЎЩњгаЁЁ ЁЁУћЃЌDРрФаЩњгаЁЁ ЁЁУћЃЌВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ3ЃЉШєДгБЛЕїВщЕФAРрКЭDРрбЇЩњжаЗжБ№ЫцЛњбЁШЁвЛЮЛЭЌбЇНјааНјвЛВНЕїВщЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЧѓГіЫљбЁЭЌбЇжаЧЁКУЪЧвЛЮЛФаЭЌбЇКЭвЛЮЛХЎЭЌбЇЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЙВга![]() Ш§ИіВПУХЃЌИљОнУПИіВПУХЕФдБЙЄШЫЪ§КЭЯргІУПШЫЫљДДЕФФъРћШѓЛцжЦГЩШчЯТЕФЭГМЦБэКЭЩШаЮЭМЃЎ
Ш§ИіВПУХЃЌИљОнУПИіВПУХЕФдБЙЄШЫЪ§КЭЯргІУПШЫЫљДДЕФФъРћШѓЛцжЦГЩШчЯТЕФЭГМЦБэКЭЩШаЮЭМЃЎ

ИїВПУХШЫЪ§МАУПШЫЫљДДФъРћШѓЭГМЦБэ
ВПУХ | дБЙЄШЫЪ§ | УПШЫЫљДДЕФФъРћШѓ/ЭђдЊ |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
ЃЈ1ЃЉЂйдкЩШаЮЭМжаЃЌCВПУХЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЮЊ___________ЃЛ
ЂкдкЭГМЦБэжаЃЌ![]() ___________ЃЌ
___________ЃЌ![]() ___________ЃЛ
___________ЃЛ
ЃЈ2ЃЉЧѓетИіЙЋЫОЦНОљУПШЫЫљДДФъРћШѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ6ЗжЃЉШчЭМЃЌЁїABCШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ2ЃЌ4ЃЉЃЌBЃЈ1ЃЌ1ЃЉЃЌCЃЈ4ЃЌ3ЃЉЃЎ

ЃЈ1ЃЉЧыЛГіЁїABCЙигкxжсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіЕуA1ЕФзјБъЃЛ
ЃЈ2ЃЉЧыЛГіЁїABCШЦЕуBФцЪБеыа§зЊ90ЁуКѓЕФЁїA2BC2ЃЛ
ЃЈ3ЃЉЧѓГіЃЈ2ЃЉжаCЕуа§зЊЕНC2ЕуЫљОЙ§ЕФТЗОЖГЄЃЈМЧЙ§БЃСєИљКХКЭІаЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧЮвЙњЙХДњЪ§бЇЕФОЕфжјзїЃЌЪщжагавЛИіЮЪЬтЃКЁАНёгаЛЦН№ОХУЖЃЌАзвјвЛЪЎвЛУЖЃЌГЦжЎжиЪЪЕШЃЎНЛвзЦфвЛЃЌН№ЧсЪЎШ§СНЃЎЮЪН№ЁЂвјвЛУЖИїжиМИКЮЃПЁБЃЎвтЫМЪЧЃКМзДќжазАгаЛЦН№9УЖЃЈУПУЖЛЦН№жиСПЯрЭЌЃЉЃЌввДќжазАгаАзвј11УЖЃЈУПУЖАзвјжиСПЯрЭЌЃЉЃЌГЦжиСНДќЯрЕШЃЎСНДќЛЅЯрНЛЛЛ1УЖКѓЃЌМзДќБШввДќЧсСЫ13СНЃЈДќзгжиСПКіТдВЛМЦЃЉЃЎЮЪЛЦН№ЁЂАзвјУПУЖИїжиЖрЩйСНЃПЩшУПУЖЛЦН№жиxСНЃЌУПУЖАзвјжиyСНЃЌИљОнЬтвтЕУЃЈЁЁЁЁЃЉ
A. ![]()
B. ![]()
C. ![]()
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
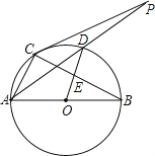
ЁОЬтФПЁП ШчЭМЃЌдВOЪЧвдABЮЊжБОЖЕФЁїABCЕФЭтНгдВЃЌDЪЧСгЛЁ![]() ЕФжаЕуЃЌСЌADВЂбгГЄгыЙ§CЕуЕФЧаЯпНЛгкЕуPЃЌODгыBCЯрНЛгкEЃЛ
ЕФжаЕуЃЌСЌADВЂбгГЄгыЙ§CЕуЕФЧаЯпНЛгкЕуPЃЌODгыBCЯрНЛгкEЃЛ
ЃЈ1ЃЉЧѓжЄЃКOE=![]() ACЃЛ
ACЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБAC=6ЃЌAB=10ЪБЃЌЧѓЧаЯпPCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com