
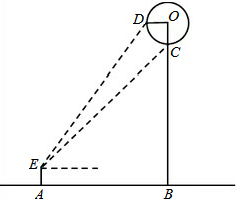
 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)| 3 |
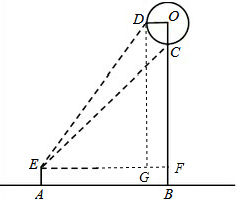 解:如图,过E点作EF⊥OB于F,过D点作DG⊥EF于G.
解:如图,过E点作EF⊥OB于F,过D点作DG⊥EF于G.| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
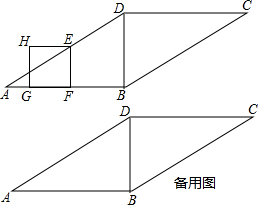
 已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)
已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com