
| 5 |
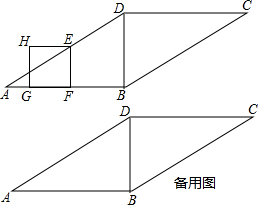
| 5 |
| DE |
| DB |
| EH |
| AB |
| t-4 |
| 4 |
| 8-t |
| 8 |
| 16 |
| 3 |
| BD |
| AB |
| EF |
| AF |
| IG |
| AG |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| AD |
| EF |
| BD |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| 3 |
| 4 |
| 16 |
| 3 |
| AB |
| BD |
| ME |
| DE |
| 1 |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| 7 |
| 4 |
| 16 |
| 3 |
| DE |
| DB |
| DP |
| DC |
| a |
| 4 |
| 8-8a |
| 8 |
| 4 |
| 5 |
| a |
| 4 |
| 8a-8 |
| 8 |
| 4 |
| 3 |
| a |
| 4 |
| 24-8a |
| 8 |
| 12 |
| 5 |
| a |
| 4 |
| 8a-24 |
| 8 |
| 24 |
| 5 |
| 16 |
| 3 |
| 32 |
| 5 |


科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
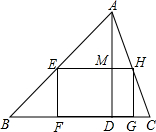 一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.
一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 列方程(组)或不等式(组)解应用题:
列方程(组)或不等式(组)解应用题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
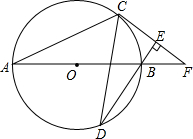 如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
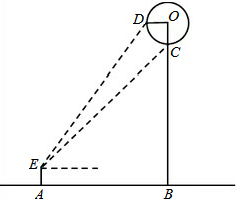 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com