
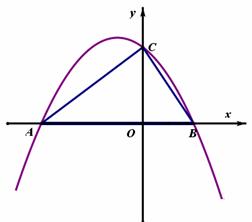
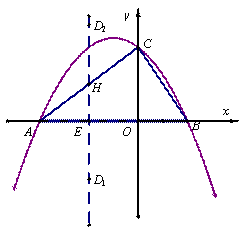
如图,抛物线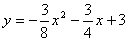 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上一动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l解析式。
解:(1)令y=0,则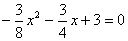 ,解得
,解得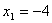 ,
,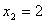
 ∴A(-4,0),B(2,0)
∴A(-4,0),B(2,0)
(2)∵抛物线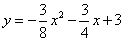 的对称轴为x=-1,与y轴交点C的坐标为(0,3)
的对称轴为x=-1,与y轴交点C的坐标为(0,3)
∴直线AC的解析式为 ,且当x=-1时,有
,且当x=-1时,有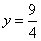
∴直线AC与对称轴x=-1的交点坐标为(-1,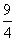 )
)
∵AB=6,CO=3
∴△ACB的面积为: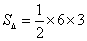 =9
=9
不妨设点D的坐标为(-1,a),当点D位于AC上方时,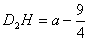 ,
,
∴△ACD的面积为: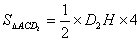 =9;解方程得:
=9;解方程得: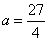
当点D位于AC下方时,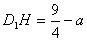 ,
,
∴△ACD的面积为: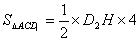 =9;解方程得:
=9;解方程得: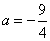 -
-
∴点D的坐标为 或
或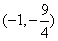
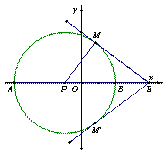
(3)如下图,以AB为直径作⊙P,当且仅当直线l与⊙P相切时符合题意,
∵Rt△PME中,∠PME=90°,PM=3,PE=5,
∴由勾股定理可得: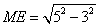 =4;利用三角形相似可以求得点M的坐标
=4;利用三角形相似可以求得点M的坐标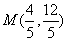
设直线l的解析式为: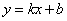 ,代入
,代入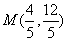 、E(4,0)可得方程组
、E(4,0)可得方程组
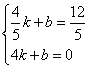 ;解方程组得:
;解方程组得: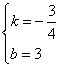
∴直线l的解析式为: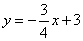
同理可得:直线l的另一个解析式为:


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
如图,点A是5×5网格图形中的一个格点,图中每个小正方形的边长为1,请在网格中按下列要求操作:
(1)以点A为其中的一个顶点,在图(1)中画一个面积等于3的格点直角三角形;
(2)以点A为其中的一个顶点,在图(2)中画一个面积等于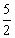 的格点等腰直角三角形.
的格点等腰直角三角形.
(3). 以点A为其中的一个顶点, 在图(3)中画一个三边比为1: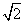 :
: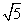 ,且最长边为5的格点三角形.
,且最长边为5的格点三角形.

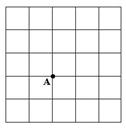

图(1) 图(2) 图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,已知点A(4,0),B(0, 3),若有一个直角三角形与Rt△OAB全等,且它们有一条公共边,请画出符合要求的图形,并直接写出这个直角三角形未知顶点的坐标(至少写5个)
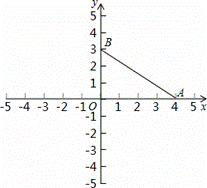
查看答案和解析>>
科目:初中数学 来源: 题型:
在“体育中考”的某次模拟测试中,某校某班10名学生测试成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是 ( )
A.众数是90 B.中位数是28 C.平均数是27.5 D.极差是8
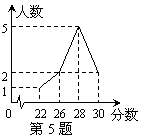

查看答案和解析>>
科目:初中数学 来源: 题型:
森林是地球之 肺,每年能为人类提供大约28.3亿吨的有机物.对于这个近似数,下列说法正确的是( )
肺,每年能为人类提供大约28.3亿吨的有机物.对于这个近似数,下列说法正确的是( )
A. 精确到十分位,有3个有效数字
B. 精确到个位,有10个有效数字
C. 精确到千万位,有3个有效数字
D. 精确到千万位,有11个有效数字
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com