
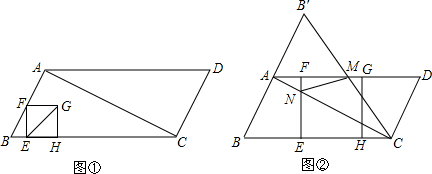
���� ��1����Rt��ABC�����AB��AC��������á�ABCD���������Rt��ABC�������t��ֵ��
��2����0��t��$\frac{10}{7}$��$\frac{10}{7}$��t��2��2��t��6��6��t��10���ۣ������غϲ���ͼ���ص㣬��t��ʾ�����߶εij��ȣ���������غϲ��ֵ��������ʽ��
��3����CM=CN��MC=MN��NM=NC����������ۣ��������ƻɶ����з��̼�����⣮
��� �⣺��1����AB=a��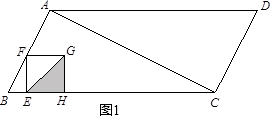
��AC��AB��tan��B=2��
��AC=2a��
��BC=10��
��a2+��2a��2=102����a=2$\sqrt{5}$��
��AB=2$\sqrt{5}$��AC=4$\sqrt{5}$��
���ABCD�����Ϊ2��$\frac{1}{2}$��2$\sqrt{5}$��4$\sqrt{5}$��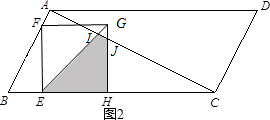
����F���A�غ�ʱ��BF=2$\sqrt{5}$��tan��B=2��
��$\frac{EF}{BE}=2$
��EF=2BE
��BE2=BF2-EF2=BF2-��2BE��2=��2$\sqrt{5}$��2-4BE2
��ã�BE=2��
��t=2��
�ʴ�Ϊ��40��2��
��2����0��t��$\frac{10}{7}$��ʱ����EHG���ABC���ص�����Ϊ��EHG��
��ͼ1��BE=t��EF=2t��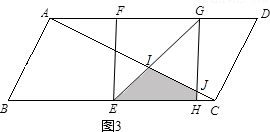
��S=$\frac{1}{2}$��2t��2t=2t2��
��$\frac{10}{7}$��t��2ʱ����EHG���ABC���ص�����Ϊ�ı���EHJI����ͼ2��
S=S��EIC-S��JHC
=$\frac{1}{2}$����10-t����$\frac{10-t}{3}$-$\frac{1}{2}$����10-3t����$\frac{10-3t}{2}$
=-$\frac{25}{12}{t}^{2}+\frac{35}{3}t-\frac{25}{3}$��
��2��t��6ʱ����EHG���ABC���ص�����Ϊ�ı���EHJI����ͼ3��
S=S��EIC-S��JHC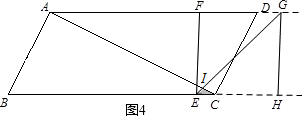
=$\frac{1}{2}$����10-t����$\frac{10-t}{3}$-$\frac{1}{2}$����6-t����$\frac{6-t}{2}$
=-$\frac{49}{12}{t}^{2}+\frac{35}{3}t-\frac{1}{3}$��
��6��t��10ʱ����EHG���ABC���ص�����Ϊ��EHJI����ͼ4��
S=$\frac{1}{2}$����10-t����$\frac{10-t}{3}$
=$\frac{1}{6}{t}^{2}-\frac{10}{3}t+\frac{50}{3}$��
����������S��t�ĺ�����ϵʽΪ��$S=\left\{\begin{array}{l}2{t^2}��0��t��\frac{10}{7}��\\-\frac{25}{12}{t^2}+\frac{35}{3}t-\frac{25}{3}��\frac{10}{7}��t��2��\\-\frac{49}{12}{t^2}+\frac{35}{3}t-\frac{1}{3}��2��t��6��\\ \frac{1}{6}{t^2}-\frac{10}{3}t+\frac{50}{3}��6��t��10��\end{array}\right.$��
��3�����ڣ�
��ͼ5������A��M��BC�Ĵ��ߣ�����ֱ�ΪI��J��
�ߵ�B���ڵ�A�ĶԳƵ�B�@��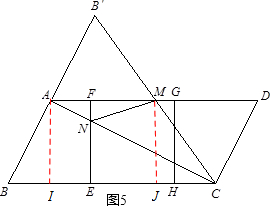
��AM�ǡ�B�@BC����λ�ߣ�
��AM=5��
��BI=2��AI=MJ=4��BE=t��
��JC=3��MC=5��EC=10-t��IC=8��
�ɡ�CNE��CAI����$\frac{NE}{AI}=\frac{EC}{IC}$����$\frac{NE}{4}=\frac{10-t}{8}$��NE=$\frac{1}{2}$��10-t����
��NC=$\frac{\sqrt{5}}{2}$��10-t����
��FM=7-t��FN=4-$\frac{1}{2}$��10-t��=$\frac{1}{2}$��t-2����
��NM=$\sqrt{��7-t��^{2}+[\frac{1}{2}��t-2��]^{2}}$��
��CM=CNʱ��$\frac{\sqrt{5}}{2}$��10-t��=5��t=10-2$\sqrt{5}$��
��MC=MNʱ��$\sqrt{��7-t��^{2}+[\frac{1}{2}��t-2��]^{2}}$=5��t=2��
��NM=NCʱ��$\sqrt{��7-t��^{2}+[\frac{1}{2}��t-2��]^{2}}$=$\frac{\sqrt{5}}{2}$��10-t����t=$\frac{15}{2}$��
������������t=10-2$\sqrt{5}$��2��$\frac{15}{2}$ʱ����MNCΪ���������Σ�
���� ���⿼���˵���涯���⣬ƽ���ı��ε����ʣ�������Ǻ������壬���ɶ�������ʵ�������к�����ϵʽ����������λ�ߵ��ж������ʣ����������ε��ж������ʣ����������ε��ж�������˼���Ӧ�ã��ۺ��Խ�ǿ����һ���Ѷȣ��ر��ǵ���������������������ε����ʣ���������϶࣬����Ҫȫ�森



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijѧУ��1500��ѧ���μ��조�Ұ����ǵĿ��á�Ϊ�����ͼƬ�������������������ȡ���ֲ���ѧ���ijɼ�����������������ͼ����ͼ��
ijѧУ��1500��ѧ���μ��조�Ұ����ǵĿ��á�Ϊ�����ͼƬ�������������������ȡ���ֲ���ѧ���ijɼ�����������������ͼ����ͼ��| ������ | Ƶ�� | Ƶ�� |
| 60��x��70 | 40 | 0.40 |
| 70��x��80 | 35 | b |
| 80��x��90 | a | 0.15 |
| 90��x��100 | 10 | c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{1}{3}}$ | B�� | $\sqrt{0.3}$ | C�� | $\sqrt{{a^2}+3}$ | D�� | $\sqrt{a{b^2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com