
 某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.40 |
| 70≤x<80 | 35 | b |
| 80≤x<90 | a | 0.15 |
| 90≤x<100 | 10 | c |
分析 (1)根据第一组的频数与频率可求出总的调查人数,然后根据第二组的频数和第三组的频率即可求出a、b、c的值;
(2)根据(1)中求出的a值,可补全频数分布直方图;
(3)优秀率=第三组和第四组的频率之和×100%;用总人数乘以优秀率,计算即可得解.
解答 解:(1)总的调查人数=$\frac{40}{0.40}$=100人,
∵第二组的频数为35,
∴b=$\frac{35}{100}$=0.35;
∵第三组的频率为0.15,
∴a=100×0.15=15.
∴c=$\frac{10}{100}$=0.1;
故答案为:15,0.35,0.1
(2)根据(1)得出的a的值,补图如下:
(3)优秀率是(0.15+0.10)×100%=25%;
该校参赛学生获得优秀的人数是:1500×25%=375人.
点评 本题考查频数分布直方图、频率分布表和用样本估计总体的知识,解题时要注意分布表和分布图相结合是本题的关键.


科目:初中数学 来源: 题型:解答题
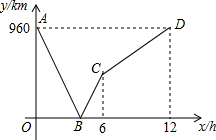 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
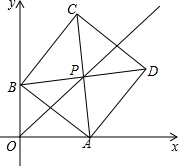 在平面直角坐标系xOy中,边长为$\sqrt{2}$的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动,顶点C、D都在第一象限.
在平面直角坐标系xOy中,边长为$\sqrt{2}$的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动,顶点C、D都在第一象限.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,商业大厦与电视台大厦的大楼顶部各有一个射灯,两条光柱的仰角(即光柱与水平面的夹角)∠2、∠3分别是60°、40°,则光柱相交时(在同一个平面内)的夹角∠1=80°.
如图,商业大厦与电视台大厦的大楼顶部各有一个射灯,两条光柱的仰角(即光柱与水平面的夹角)∠2、∠3分别是60°、40°,则光柱相交时(在同一个平面内)的夹角∠1=80°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com