
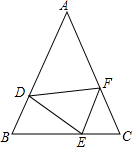
 如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、CA上的点,且BD=CE,∠DEF=∠B.求证:DE=EF.
如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、CA上的点,且BD=CE,∠DEF=∠B.求证:DE=EF. 分析 如图,首先运用等腰三角形的性质、三角形的内角和定理来证明∠BDE=∠CEF,此为解决问题的关键性结论;运用ASA公理证明△BDE≌△CEF,即可解决问题.
解答  证明:如图,∵AB=AC,
证明:如图,∵AB=AC,
∴∠B=∠C;而∠DEF=∠B,
∴∠B=∠DEF=∠C,
∴∠BDE+∠BED=∠BED+∠CEF,
∴∠BDE=∠CEF;在△BDE与△CEF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{BD=CE}\\{∠BDE=∠CEF}\end{array}\right.$,
∴△BDE≌△CEF(ASA),
∴DE=EF.
点评 该题主要考查了三角形的内角和定理、全等三角形的判定及其性质等几何知识点及其应用问题;牢固掌握三角形的内角和定理、全等三角形的判定及其性质等几何知识点是基础,灵活运用、解题是关键.


科目:初中数学 来源: 题型:填空题
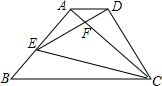 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD; ②△ACD∽△BCE; ③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为$\frac{3}{8}$.其中正确的结论是①②④⑤.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD; ②△ACD∽△BCE; ③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为$\frac{3}{8}$.其中正确的结论是①②④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
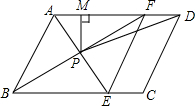 如图所示,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF、PD.
如图所示,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF、PD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.40 |
| 70≤x<80 | 35 | b |
| 80≤x<90 | a | 0.15 |
| 90≤x<100 | 10 | c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com