
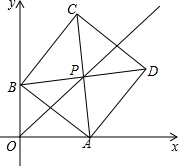
 在平面直角坐标系xOy中,边长为$\sqrt{2}$的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动,顶点C、D都在第一象限.
在平面直角坐标系xOy中,边长为$\sqrt{2}$的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动,顶点C、D都在第一象限.分析 (1)当∠BAO=45°时,因为四边形ABCD是正方形,P是AC,BD对角线的交点,能证明OAPB是正方形,从而求出P点的坐标.
(2)过P点作x轴和y轴的垂线,可通过三角形全等,证明是角平分线.
(3)根据垂线段最短,点B与点O重合时,点A与点O重合时,点P到y轴的距离最小,为正方形ABCD边长的一半,OA=B时点P到y轴的距离最大,为PB的长度,即可得解.
解答 解:(1)∵∠BPA=90°,PA=PB,
∴∠PAB=45°,
∵∠BAO=45°,
∴∠PAO=90°,
∴四边形OAPB是正方形,
∵AB=$\sqrt{2}$,由勾股定理得:PA=PB=1
∴P点的坐标为:(1,1).
(2)证明:如图,作PE⊥x轴交x轴于E点,作PF⊥y轴交y轴于F点,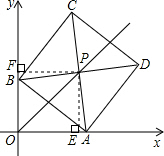
∵∠BPE+∠EPA=90°,∠EPB+∠FPB=90°,
∴∠FPB=∠EPA,
在△PBF和△PAE中,
$\left\{\begin{array}{l}{∠FPB=∠EPA}\\{∠PFB=∠PEA}\\{BP=AP}\end{array}\right.$,
∴△PBF≌△PAE(AAS),
∴PE=PF,
∴点P在∠AOB的平分线上.
(3)解:当点B与点O重合时,点A与点O重合时,点P到y轴的距离最小,
d=$\frac{1}{2}$×$\sqrt{2}$=$\frac{\sqrt{2}}{2}$,
当OA=OD时,点P到y轴的距离最大,d=PB=1,
∵点A,B都不与原点重合,
∴$\frac{\sqrt{2}}{2}$<d≤1,
故答案为:$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}<d≤1$.
点评 本题考查了正方形的性质,坐标与图形的性质,全等三角形的判定与性质,角平分线的判定,(2)作辅助线构造出全等三角形是解题的关键,(2)根据垂线段最短判断出最小与最大值的情况是解题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
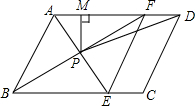 如图所示,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF、PD.
如图所示,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF、PD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.40 |
| 70≤x<80 | 35 | b |
| 80≤x<90 | a | 0.15 |
| 90≤x<100 | 10 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
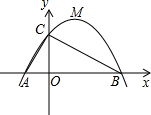 如图:函数y=ax2+bx+c(其中a、b、c为常数)的图象分别与x轴、y轴交于A、B、C三点,M为抛物线的顶点,位于一象限,且AC⊥BC,OA<OB.
如图:函数y=ax2+bx+c(其中a、b、c为常数)的图象分别与x轴、y轴交于A、B、C三点,M为抛物线的顶点,位于一象限,且AC⊥BC,OA<OB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\frac{1}{{\sqrt{2}}}$ | C. | $\sqrt{2}$ | D. | $\sqrt{0.2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com