
分析 (1)利用待定系数法求一次函数的解析式;
(2)设每天获得的利润为W元,根据总利润=每天的销售量y×(售价-成本),代入可求得解析式,并求最值即可.
解答 解:(1)设y与x之间的函数关系式:y=kx+b,
把(22,780)、(25,750)代入得:$\left\{\begin{array}{l}{22k+b=780}\\{25k+b=750}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-10}\\{b=1000}\end{array}\right.$,
则y与x之间的函数关系式:y=-10x+1000;
(2)设工艺厂销售该工艺品每天获得的利润为W元,
W=y(x-20)=(-10x+1000)(x-20)=-10x2+1200x-20000,
W=-10(x2-120x+3600-3600)-20000=-10(x-60)2+16000,
∵-10<0,
∴W有最大值,
当x=60时,W有最大值是16000元;
则该工艺品的售价定为每件60元时,每天获得的利润最大,最大利润是16000元.
点评 本题是二次函数的应用,属于销售利润问题,此类题要明确总利润=销售量×单件利润;单件利润=售价-成本;对于最值问题,一般情况下,就是二次函数的顶点坐标的纵坐标.


科目:初中数学 来源: 题型:解答题
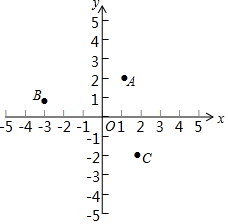 在平面直角坐标系中,对于任意三点A,B,C,我们给出如下定义:
在平面直角坐标系中,对于任意三点A,B,C,我们给出如下定义:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
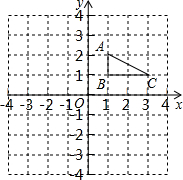 △ABC在平面直角坐标系中的位置如图所示,其中A(1,2),B(1,1),C(3,1),画出△ABC绕原点O顺时针旋转90°后得到△A′B′C′.
△ABC在平面直角坐标系中的位置如图所示,其中A(1,2),B(1,1),C(3,1),画出△ABC绕原点O顺时针旋转90°后得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com