
分析 (1)直接化简二次根式,再结合完全平方公式合并进而求出答案;
(2)直接利用加减消元法解方程得出答案.
解答 解:(1)$\frac{\sqrt{18}+\sqrt{2}}{\sqrt{2}}$-3+(3+$\sqrt{2}$)2
=$\frac{4\sqrt{2}}{\sqrt{2}}$-3+3+2+6$\sqrt{2}$
=6+6$\sqrt{2}$;
(2)$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1①}\\{3x+2y=10②}\end{array}\right.$,
①×6-②得:
-2(y+1)-2y=-4,
解得:y=$\frac{1}{2}$,
则3x+2×$\frac{1}{2}$=10,
解得:x=3,
故方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=\frac{1}{2}}\end{array}\right.$.
点评 此题主要考查了二次根式的混合运算以及二元一次方程组的解法,正确化简二次根式是解题关键.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
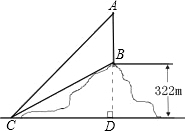 江郎山位我国典型的丹霞地貌景观,被称为“中国丹霞第一奇峰”.要测量三块巨石中的最左边的“郎峰”的高度,在山脚的平地上选取一处观测点C,测得∠BCD=30°,∠ACD=45°,已知从观测点C到“郎峰”脚B的垂直高度为322米,如图所示,那么“郎峰”AB的高度约为多少?
江郎山位我国典型的丹霞地貌景观,被称为“中国丹霞第一奇峰”.要测量三块巨石中的最左边的“郎峰”的高度,在山脚的平地上选取一处观测点C,测得∠BCD=30°,∠ACD=45°,已知从观测点C到“郎峰”脚B的垂直高度为322米,如图所示,那么“郎峰”AB的高度约为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年龄x | 生存人数l | 死亡人数d |
| 0 | 1000000 | 661 |
| 1 | 999339 | 536 |
| 30 | 991476 | 403 |
| 31 | 991074 | 428 |
| 61 | 938005 | 6064 |
| 62 | 931941 | 6743 |
| 63 | 925198 | 7489 |
| 64 | 917709 | 8314 |
| 79 | 649175 | 32429 |
| 80 | 616746 | 34398 |
| 81 | 582347 | 36253 |
| 82 | 546095 | 37950 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com