
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且![]() ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
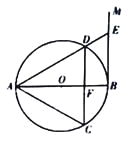
(l)求证:△ACD是等边三角形;
(2)连接OE,若DE=2,求OE的长.
【答案】(1)见解析(2)![]()
【解析】试题(1)根据切线的定义可知AB⊥BM,又∵BM//CD,∴AB⊥CD,根据圆的对称性可得AD=AC,再根据等弧对等弦得DA=DC,即DA=DC=AC,所以可得△ACD是等边三角形;(2)△ACD为等边三角形,AB⊥CD,由三线合一可得∠DAB=30°,连接BD,根据直径所对的角是直角和三角形的内角和可得∠∠EBD=∠DAB=30°,因为DE=2,求出BE=4,根据勾股定理得![]() ,直角三角形中30°角所对的直角边等于斜边的一半得,
,直角三角形中30°角所对的直角边等于斜边的一半得, ![]() ,
, ![]() ,在Rt△OBE中,根据勾股定理即可得出OE的长.
,在Rt△OBE中,根据勾股定理即可得出OE的长.
试题解析:证:∵BM是⊙O切线,AB为⊙O直径,∴AB⊥BM,∵BM//CD,∴AB⊥CD,
∴AD=AC,∴AD=AC,∴DA=DC,∴DC=AD,∴AD=CD=AC,∴△ACD为等边三角形.
证:(2)△ACD为等边三角形,AB⊥CD,∴∠DAB=30°,连结BD,∴BD⊥AD.
∠EBD=∠DAB=30°,∵DE=2,∴BE=4, ![]() ,
, ![]() ,
, ![]() ,
,
在Rt△OBE中, ![]() .
.



科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为( )
,那么该矩形的周长为( )

A. 72cm B. 36cm C. 20cm D. 16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点![]() ,
,![]() 分别是锐角
分别是锐角![]() 两边上的点,
两边上的点,![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,以
为圆心,以![]() 的长为半径画弧,两弧相交于点
的长为半径画弧,两弧相交于点![]() ,连接
,连接![]() ,
,![]() .则根据作图过程判定四边形
.则根据作图过程判定四边形![]() 是菱形的依据是______.
是菱形的依据是______.
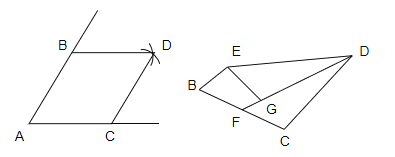
(2)如图,在菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
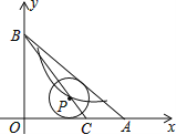
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
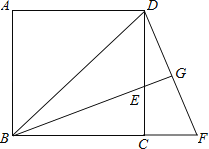
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形ABC中,∠BAC=90°,AB=AC=2,直角三角板含45°角的顶点P在边BC上移动(点P不与B,C重合),如图,直角三角板的一条直角边始终经过点A,斜边与边AC交于点Q,当△ABP为等腰三角形时,CQ的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
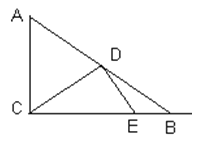
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AB=10,tanA=4/3,点D是斜边AB上的动点,连接CD,作DE⊥CD,交射线CB于点E,设AD=x。(1)当点D是边AB的中点时,求线段DE的长;(2)当△BED是等腰三角形时,求x的值;(3)如果y=DE/DB。求y关于x的函数解析式,并写出它的定义域。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com