
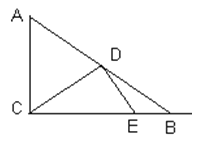
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AB=10,tanA=4/3,点D是斜边AB上的动点,连接CD,作DE⊥CD,交射线CB于点E,设AD=x。(1)当点D是边AB的中点时,求线段DE的长;(2)当△BED是等腰三角形时,求x的值;(3)如果y=DE/DB。求y关于x的函数解析式,并写出它的定义域。
【答案】(1)DE=![]() ;(2)(i)x=
;(2)(i)x=![]() ;(ii)AD=2;(3)y=
;(ii)AD=2;(3)y=![]() (0<x<10).
(0<x<10).
【解析】
试题(1)在直角三角形ABC中,由AB与tanA的值,利用锐角三角函数定义及勾股定理求出BC与AC的长,由D为斜边上的中点,利用直角三角形斜边上的中线等于斜边的一半得到CD=AD=BD=5,可得出∠DCB=∠DBC,再由一对直角相等,利用两对对应角相等的三角形相似得到△EDC与△ACB相似,由相似得比例,即可求出DE的长;
(2)分两种情况考虑:
(i)当E在BC边上时,由△BDE为等腰三角形且∠BED为钝角,得到DE=BE,利用等边对等角得到∠EBD=∠EDB,利用等角的余角相等得到∠CDA=∠A,利用等角对等边得到CD=AC,作CH垂直于AB,利用三线合一得到AD=2AH,由cosA的值求出AH的长,进而求出AD的长,即为x的值;
(ii)当E为BC延长线上时,与∠DBE为钝角得到DB=BE,同理求出x的值;
(3)作DM垂直于BC,得到DM与AC平行,由平行得比例,表示出DM与BM,进而表示出CD与CM,由三角形DEM与三角形CDM相似得比例,表示出DE,由BD=AB-AD=10-x,将DE与DB代入表示出y,化简得到结果,并求出x的范围即可.
试题解析:
(1)在△ABC中,∵∠ACB=90°,AB=10,tanA="4" 3 ,
∴BC=8,AC=6,
∵点D为斜边AB的中点,∴CD=AD=BD=5,
∴∠DCB=∠DBC,
∵∠EDC=∠ACB=90°,
∴△EDC∽△ACB,
∴DE:CD="AC:BC" ,即DE:5="6:8" ,
则DE=![]() ;
;
(2)分两种情况情况:
(i)当E在BC边长时,
∵△BED为等腰三角形,∠BED为钝角,
∴EB=ED,
∴∠EBD=∠EDB,
∵∠EDC=∠ACB=90°,
∴∠CDA=∠A,
∴CD=AC,
作CH⊥AB,垂足为H,那么AD=2AH,
∴AH:AC="3:5" ,即AH=![]() ,
,
∴AD=![]() ,即x=
,即x=![]() ;
;
(ii)当E在CB延长线上时,
∵△BED为等腰三角形,∠DBE为钝角,
∴BD=DE,
∴∠BED=∠BDE,
∵∠EDC=90°,
∴∠BED+∠BCD=∠BDE+∠BDC=90°,
∴∠BCD=∠BDC,
∴BD=BC=8,
∴AD=x=AB-BD=10-8=2;
(3)作DM⊥BC,垂足为M,
∵DM∥AC,
∴DM:AC="BM:BC=BD:BA" ,
∴DM=![]() (10-x),BM=
(10-x),BM=![]() (10-x),
(10-x),
∴CM=8-![]() (10-x)=
(10-x)=![]() x,CD= x2
x,CD= x2![]() x+36 ,
x+36 ,
∵△DEM∽△CDM,/span>
∴DE:DM="CD:CM" ,即DE=![]() ,
,
∴y=![]() ,
,
整理得:y=![]() (0<x<10).
(0<x<10).


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且![]() ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
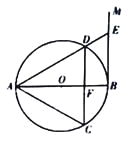
(l)求证:△ACD是等边三角形;
(2)连接OE,若DE=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时都以同样价格出售相同的商品,“五一”期间两家商场都让利酬宾.其中甲商场所有商品直接打折销售,乙商场在购买一定数额商品后,超过部分打折售.设商品的原价为![]() 元,购买商品后实付金额为
元,购买商品后实付金额为![]() 元,
元,![]() 与
与![]() 之间的函数关系如图所示:
之间的函数关系如图所示:

(1)求![]() 的值;
的值;
(2)说出甲乙两家商场的具体销售方式;
(3)“五一”期间,选择哪家商场去购物更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
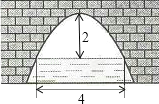
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
A.3 B.2![]() C.3
C.3![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中, ![]() ,D、E是斜边BC上两点,且∠DAE=45°,将△
,D、E是斜边BC上两点,且∠DAE=45°,将△![]() 绕点
绕点![]() 顺时针旋转90
顺时针旋转90![]() 后,得到△
后,得到△![]() ,连接
,连接![]() .列结论:
.列结论:
①△ADC≌△AFB;②△ ![]() ≌△
≌△![]() ;③△
;③△![]() ≌△
≌△![]() ;④
;④![]()
其中正确的是( )

A. ②④ B. ①④ C. ②③ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
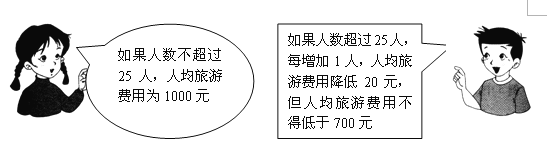 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
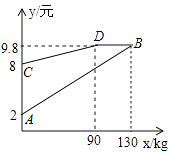
【题目】2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
(1)请你解释图中点B的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的y1与x之间的函数解析式;
(3)当0<x≤90时,求该葵花籽的产量为多少时,该企业获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
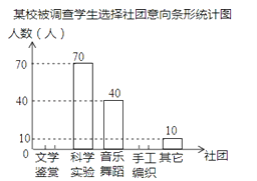
【题目】为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,△ABC中,∠ACB=90°,D.E分别是BC、BA的中点,联结DE,F在DE延长线上,且AF=AE.
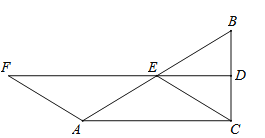
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com