
【题目】(7分)如图,△ABC中,∠ACB=90°,D.E分别是BC、BA的中点,联结DE,F在DE延长线上,且AF=AE.
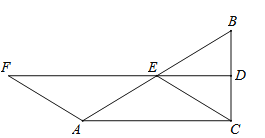
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
【答案】(1)证明见试题解析;(2)30°.
【解析】
试题(1)由直角三角形斜边上的中线等于斜边的一半,得到CE=AE=BE,从而得到AF=CE,再由等腰三角形三线合一,得到∠1=∠2,从而有∠F=∠3,得到∠2=∠F,故CE∥AF,然后利用一组对边平行且相等的四边形是菱形证明;
(2)由菱形的性质,得到AC=CE,求出AC=CE=AE,从而得到△AEC是等边三角形,得出∠CAE=60°,然后根据直角三角形两锐角互余解答.
试题解析:(1)∵∠ACB=90°,E是BA的中点,∴CE=AE=BE,∵AF=AE,∴AF=CE,在△BEC中,∵BE=CE且D是BC的中点,∴ED是等腰△BEC底边上的中线,∴ED也是等腰△BEC的顶角平分线,∴∠1=∠2,∵AF=AE,∴∠F=∠3,∵∠1=∠3,∴∠2=∠F,∴CE∥AF,又∵CE=AF,∴四边形ACEF是平行四边形;
(2)∵四边形ACEF是菱形,∴AC=CE,由(1)知,AE=CE,∴AC=CE=AE,∴△AEC是等边三角形,∴∠CAE=60°,在Rt△ABC中,∠B=90°﹣∠CAE=90°﹣60°=30°.


科目:初中数学 来源: 题型:
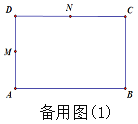
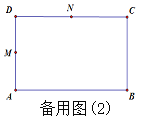
【题目】在矩形ABCD中AB=16,AD=12,点M是AD的中点,点N是CD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,速度为2单位长度/秒,点Q从N点出发沿N→C→B→A的路线匀速运动,速度为1单位长度/秒,P、Q两点同时运动,时间为t秒,若其中一点到达终点,另一点也随即停止运动.
(1)如图1,若矩形ABCD与∠PMA重叠部分的面积为y.
①求当t=4,10,16时,y的值.
②求y关于t的函数解析式.
(2)当以M、D、P、Q四个点为顶点的四边形是平行四边形时,求出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,E为对角线AC延长线上的一点.
ABCD中,E为对角线AC延长线上的一点.
(1)若四边形ABCD是菱形,求证:BE=DE.
(2)写出(1)的逆命题,并判断其是真命题还是假命题,若是真命题,给出证明;若是假命题,举出反例.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点,当AB:AD=___________时,四边形MENF是正方形.
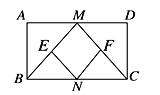
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( ) 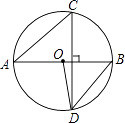
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校科技创新兴趣小组用他们设计的机器人,在平坦的操场上进行走展示.输入指令后,机器人从出发点A先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米到达终止点B.求终止点B与原出发点A的距离AB.
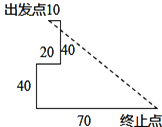
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m 
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com