
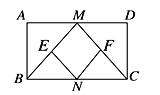
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点,当AB:AD=___________时,四边形MENF是正方形.
【答案】1:2
【解析】
试题当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形,
故答案为:1:2.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别 | 分组 | 频数 | 频率 |
1 | 50≤x<60 | 9 | 0.18 |
2 | 60≤x<70 | a | |
3 | 70≤x<80 | 20 | 0.40 |
4 | 80≤x<90 | 0.08 | |
5 | 90≤x≤100 | 2 | b |
合计 |
请根据以上频率分布表和频率分布直方图,回答下列问题: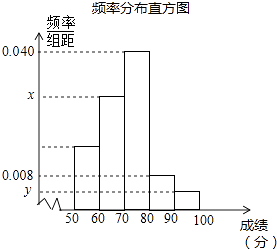
(1)求出a、b、x、y的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E. 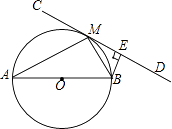
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE= ![]() ,sin∠BAM=
,sin∠BAM= ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )

A. 17 B. 18 C. 19 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,△ABC中,∠ACB=90°,D.E分别是BC、BA的中点,联结DE,F在DE延长线上,且AF=AE.
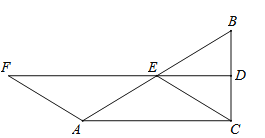
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心![]() ,再从中心
,再从中心![]() 走到正方形
走到正方形![]() GFH的中点
GFH的中点![]() ,又从中心
,又从中心![]() 走到正方形
走到正方形![]() IHJ的中心
IHJ的中心![]() ,再从中心
,再从中心![]() 走到正方形
走到正方形![]() KJP的中心
KJP的中心![]() ,一共走了
,一共走了![]() m,则长方形花坛ABCD的周长是( )
m,则长方形花坛ABCD的周长是( )

A. 36m B. 48m C. 96m D. 60m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证: 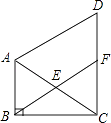
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com