解:(1)△DAC≌△ADE.
证明:∵AC=AB,
∴∠C=∠B.
∵AC为⊙O的切线,
∴∠B=∠E=∠1,
∴∠C=∠1=∠E.又

,
∴∠2=∠3.
又∠ADB=∠C+∠1,即∠2+∠3=∠C+∠1.
∴∠1=∠2=∠3=∠B=∠C=∠E.
在△DAC和△ADE中,
∵∠C=∠E,∠1=∠2,DA=AD,
∴△DAC≌△ADE.
(2)存在,它们分别为平行四边形ACDE和梯形ACDF.
证明:∵∠C=∠3,∠E=∠3,
∴AC∥DE,AE∥CD.
∴四边形ACDE是平行四边形.又AF与CD相交,
∴四边形ACDF为梯形.
分析:(1)根据圆的切线性质可求出∠B、∠C,然后求出∠2=∠3,然后利用全等三角形的判定求证.
(2)利用平行四边形以及梯形的有关知识,先说明四边形ACDE是平行四边形,再说明四边形ACDE是梯形.
点评:本题综合考查了利用圆的性质和全等三角形的判定的知识进行有关计算的能力,属于基础题,解答这类题时一般采取利用图形的全等的知识将分散的图形集中在一起,再结合图形的特征求解.

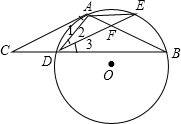 如图,AB是⊙O的弦,AC切⊙O于点A,AC=AB,CB交⊙O于点D,点E为弧AB的中点,连接AD,在不添加辅助线的情况下.
如图,AB是⊙O的弦,AC切⊙O于点A,AC=AB,CB交⊙O于点D,点E为弧AB的中点,连接AD,在不添加辅助线的情况下. ,
,
