
分析 (1)根据整式的除法,即可解答;
(2)按照多项式乘以多项式,即可解答;
(3)利用完全平方公式,平方差公式,即可解答.
解答 解:(1)4a${\;}^{\frac{2}{3}}$b${\;}^{-\frac{1}{3}}$÷(-$\frac{2}{3}$a${\;}^{-\frac{1}{3}}$b${\;}^{-\frac{1}{3}}$)
=-6ab0
=-6a.
(2)(2x${\;}^{\frac{1}{2}}$+3y${\;}^{-\frac{1}{4}}$)(2x${\;}^{-\frac{1}{2}}$-3y${\;}^{-\frac{1}{4}}$);
=4x-6${x}^{\frac{1}{2}}{y}^{-\frac{1}{4}}$+6${x}^{-\frac{1}{2}}{y}^{-\frac{1}{4}}$-9${y}^{-\frac{1}{2}}$.
(3)(a2-2+a-2)÷(a2-a-2)
=(a+a-1)2÷(a+a-1)(a-a-1)
=$\frac{{a}^{2}+1}{{a}^{2}-1}$
点评 本题考查了负整数指数幂,解决本题的关键是熟记负整数指数幂的法则.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
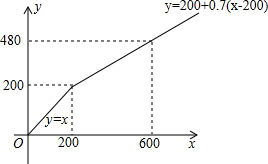 甲、乙两商场春节期间都进行让利酬宾活动.其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下y关于x的函数图象,x(单位:元)表示商品原价,y(单位:元)表示购物金额.若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并说明如何选择这两家商场购物更省钱.
甲、乙两商场春节期间都进行让利酬宾活动.其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下y关于x的函数图象,x(单位:元)表示商品原价,y(单位:元)表示购物金额.若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并说明如何选择这两家商场购物更省钱.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
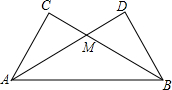 把两个同样大小的含30度的三角尺像如图所示那样放置,其中M是AD与BC的交点.证明:
把两个同样大小的含30度的三角尺像如图所示那样放置,其中M是AD与BC的交点.证明:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
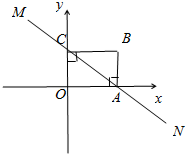 直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.
直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com