练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

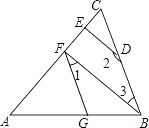
    【题目】如图，∠AGF=∠ABC，∠1+∠2=180°．

    (1)试判断BF与DE的位置关系，并说明理由；

    (2)若BF⊥AC，∠2=150°，求∠AFG的度数．

    【答案】（1）BF∥DE，理由见解析；（2）60°.

    【解析】试题分析：（1）由于∠AGF=∠ABC，可判断GF∥BC，则∠1=∠3，由∠1+∠2=180°得出∠3+∠2=180°判断出BF∥DE；

    （2）由BF∥DE，BF⊥AC得到DE⊥AC，由∠2=150°得出∠1=30°，得出∠AFG的度数

    解：（1）BF∥DE，理由如下：

    ∵∠AGF=∠ABC，

    ∴GF∥BC，

    ∴∠1=∠3，

    ∵∠1+∠2=180°，

    ∴∠3+∠2=180°，

    ∴BF∥DE；

    （2）∵BF∥DE，BF⊥AC，

    ∴DE⊥AC，

    ∵∠1+∠2=180°，∠2=150°，

    ∴∠1=30°，

    ∴∠AFG=90°﹣30°=60°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知直线y=﹣x+2分别交x、y轴于点A、B，点C为线段OA的中点，动点P从坐标原点出发，以2个单位长度/秒的速度向终点A运动，动点Q从点C出发，以个单位长度/秒的速度向终点B运动．过点Q作QM∥AB交x轴于点M，动点P、Q同时出发，其中一个点到达终点，另一个点也停止运动，设点P运动的时间为t秒，PM的长为y个单位长度．

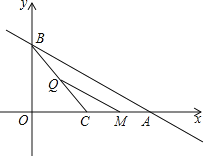
    （1）∠BCO= °；

    （2）求y关于t的函数关系式及自变量t的取值范围；

    （3）是否存在时间t，使得以PC为直径的⊙D与直线QM相切？若存在，求t的值；不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等腰△ABC中，AB=AC，∠A=50°，则∠B= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

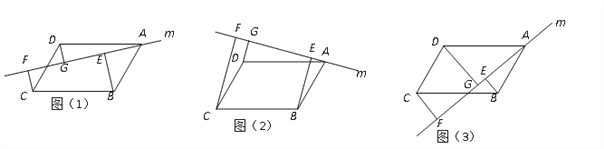
    【题目】已知□ABCD中，直线m绕点A旋转，直线m不经过B、C、D点，过B、C、D分别作BE⊥m于E， CF⊥m于F， DG⊥m于G．

    （1）当直线m旋转到如图1位置时，线段BE、CF、DG之间的数量关系是 _；

    （2）当直线m旋转到如图2位置时，线段BE、CF、DG之间的数量关系是 _；

    （3）当直线m旋转到如图3的位置时，线段BE、CF、DG之间有怎样的数量关系？请直接写出你的猜想，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算或变形正确的是（ ）
    A.﹣2a+2b=﹣2（a+b）
    B.a2﹣2a+4=（a﹣2）2
    C.（2a2）3=6a6
    D.3a22a3=6a5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的文字，解答问题：

    大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用-1来表示的小数部分，你同意小明的表示方法吗？

    事实上，小明的表示方法是有道理，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分．

    又例如：∵，即，

    ∴的整数部分为2，小数部分为（-2）．

    请解答：（1） 的整数部分是 ，小数部分是 .

    （2）如果的小数部分为a， 的整数部分为b，求a+b-的值；

    （3）已知： 10+=x+y，其中x是整数，且0＜y＜1，求x-y的相反数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列式子成立的是（ ）
    A.﹣1+1=0
    B.﹣1﹣1=0
    C.0﹣5=5
    D.（+5）﹣（﹣5）=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E在直线DF上，点B在直线AC上，若∠1＝∠2，∠3＝∠4，则∠A＝∠F，请说明理由．

    解：∵∠1＝∠2（已知）

    ∠2＝∠DGF（ ）

    ∴∠1＝∠DGF

    ∴BD∥CE（ ）

    ∴∠3＋∠C＝180（ ）

    又∵∠3＝∠4（已知）

    ∴∠4＋∠C＝180

    ∴ ∥ （同旁内角互补，两直线平行）

    ∴∠A＝∠F（ ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将抛物线y=3x2向上平移3个单位，再向右平移2个单位，那么得到的抛物线的解析式为（ ）
    A.y=3（x+2）2+3
    B.y=3（x﹣2）2+3
    C.y=3（x+2）2﹣3
    D.y=3（x﹣2）2﹣3

    查看答案和解析>>

    同步练习册答案