
【题目】已知直线y=﹣![]() x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以
x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以![]() 个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
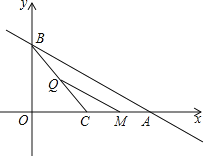
(1)∠BCO= °;
(2)求y关于t的函数关系式及自变量t的取值范围;
(3)是否存在时间t,使得以PC为直径的⊙D与直线QM相切?若存在,求t的值;不存在,说明理由.
【答案】(1)45;(2)y=2﹣t(0≤t≤2)(3)当t=1﹣![]() 或t=1+
或t=1+![]() 时,以PC为直径的⊙D与直线QM相切
时,以PC为直径的⊙D与直线QM相切
【解析】
试题分析:(1)先分别求得点A和点B的坐标,从而得到点C的坐标,从而得到OB=OC,于是可求得∠BCO的度数;
(2)先由相似三角形的性质得到CM的长,然后依据PM=CO+CM﹣OP可求得y与t的函数关系式;
(3)当点P在点C的左边时,可求得DM=1,由tan∠NMD=![]() ,可求得DN=
,可求得DN=![]() ,然后可求得DC=1﹣t,从而可求得t的值;当点P在点C的右侧时,可求得DC=t﹣1,DN=
,然后可求得DC=1﹣t,从而可求得t的值;当点P在点C的右侧时,可求得DC=t﹣1,DN=![]() ,从而可求得t的值.
,从而可求得t的值.
解:(1)∵令y=0得﹣![]() x+2=0,解得:x=4,
x+2=0,解得:x=4,
∴A(0,4).
∴OA=4.
∵点C为线段OA的中点,
∴OC=2.
∵令x=0得:y=2,
∴B(0,2).
∴OB=2.
∴OB=OC.
又∵∠BOC=90°,
∴∠BCO=45°.
故答案为:45.
(2)如图1所示:

∵OB=CO=2,∠BOC=90°,
∴BC=![]() OB=2
OB=2![]() .
.
∵OA=4,OC=2,
∴AC=2.
设点P和点Q的运动时间为t,则OP=2t,QP=![]() t.
t.
∵QM∥AB,
∴![]() ,即
,即![]() ,解得CM=t.
,解得CM=t.
∴PM=CO+CM﹣OP=2+t﹣2t=2﹣t(0≤t≤2).
∴y与t的函数关系是为y=2﹣t(0≤t≤2).
(3)如图2所示:设N为切线,连接DN.
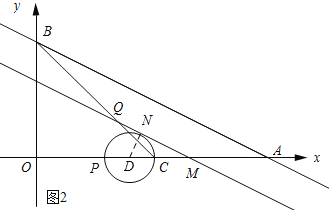
∵OP=2t,OC=2,
∴PC=2﹣2t.
∴PD=DC=1﹣t.
∴DM=PM﹣PD=2﹣t﹣(1﹣t)=1.
∵MQ是圆D的切线,
∴DN⊥QM.
∵OB=2,OA=4,
∴tan∠BAO=![]() .
.
∵QM∥AB,
∴tan∠NMP=![]() .
.
∴DN=![]() DM=
DM=![]() .
.
∴1﹣t=![]() ,解得:t=1
,解得:t=1![]() .
.
如图3所示:设N为切线,连接DN.

∵OP=2t,OC=2,
∴PC=2t﹣2.
∴DC=DP=t﹣1.
∴DM=t﹣1+2﹣t=1.
∴DN=![]() .
.
∴t﹣1=![]() ,解得:t=1+
,解得:t=1+![]() .
.
综上所述,当t=1﹣![]() 或t=1+
或t=1+![]() 时,以PC为直径的⊙D与直线QM相切.
时,以PC为直径的⊙D与直线QM相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°,AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:
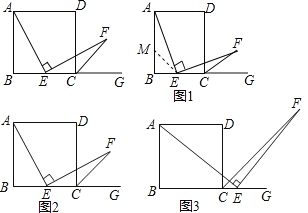
(1)经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐及水面,已知红莲移动的水平距离为2米,这里的水深为( )米.
A.1.5
B.2
C.2.5
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地去年财政收入取得重大突破,地方公共财政收入用四舍五入取近似值后为27.39亿元,那么这个数值( )
A. 精确到亿位 B. 精确到百分位
C. 精确到千万位 D. 精确到百万位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
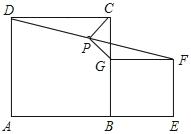
问题:如图所示,在正方形ABCD和BEFG中,点A,B,E在同一直线上,P是线段DF中点,连接PG,PC.
探究:当PG与PC的夹角为90°时,平行四边形BEFG是正方形.
小聪同学的思路是:首先可以证明四边形BEFG是矩形,然后延长GP交DC于点H,构造全等三角形,经过推理可以探索出问题答案.
请你参考小聪同学的思路,探究并解决这个问题.
(1)求证:四边形BEFG是矩形;
(2)求证:PG与PC的夹角为90°时,四边形BEFG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
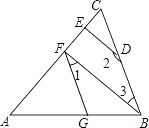
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com