Question

【题目】如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．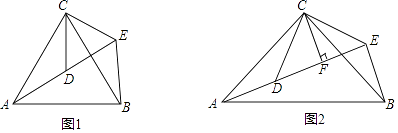

（1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°．
①求证：AD=BE；
②求∠AEB的度数．
（2）如图2，若∠ACB=∠DCE=90°，CF为△DCE中DE边上的高，试猜想AE，CF，BE之间的关系，并证明你的结论．

Answer 1

【答案】
（1）

①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°，

∴∠ACB=∠DCE=180°﹣2×50°=80°，

∵∠ACB=∠ACD_∠DCB，∠DCE=∠DCB+∠BCE，

∴∠ACD=∠BCE，

∵△ACB，△DCE都是等腰三角形，

∴AC=BC，DC=EC，

在△ACD和△BCE中，

，

∴△ACD≌△BCE（SAS），

∴AD=BE．

②解：∵△ACD≌△BCE，

∴∠ADC=∠BEC，

∵点A、D、E在同一直线上，且∠CDE=50°，

∴∠ADC=180°﹣∠CDE=130°，

∴∠BEC=130°，

∵∠BEC=∠CED+∠AEB，∠CED=50°，

∴∠AEB=∠BEC﹣∠CED=80°

（2）

解：结论：AE=2CF+BE．

理由：∵△ACB，△DCE都是等腰直角三角形，

∴∠CDE=∠CED=45°，

∵CF⊥DE，

∴∠CFD=90°，DF=EF=CF，

∵AD=BE，

∴AE=AD+DE=BE+2CF．

【解析】（1）①欲证明AD=BE，只要证明△ACD≌△BCE即可．②由△ACD≌△BCE，推出∠ADC=∠BEC，由点A、D、E在同一直线上，且∠CDE=50°，推出∠ADC=180°﹣∠CDE=130°，推出∠BEC=130°，根据∠AEB=∠BEC﹣∠CED计算即可．（2）由（1）可知AD=BE，只要证明DE=2CF即可解决问题．