
| 2 |

| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
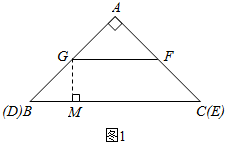
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
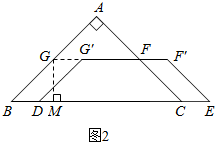
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(2
| ||||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
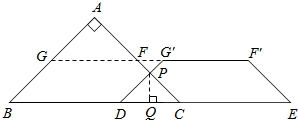
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |


 Íđ┐╝ŻÔÂ┴┐╝ÁŃżź┴̤Á┴đ┤░Ş
Íđ┐╝ŻÔÂ┴┐╝ÁŃżź┴̤Á┴đ┤░Ş
| ─ŕ╝ | Ş▀Íđ┐╬│╠ | ─ŕ╝ | │§Íđ┐╬│╠ |
| Ş▀Ď╗ | Ş▀Ď╗├ÔĚĐ┐╬│╠═Ă╝÷úí | │§Ď╗ | │§Ď╗├ÔĚĐ┐╬│╠═Ă╝÷úí |
| Ş▀Â■ | Ş▀Â■├ÔĚĐ┐╬│╠═Ă╝÷úí | │§Â■ | │§Â■├ÔĚĐ┐╬│╠═Ă╝÷úí |
| Ş▀╚ř | Ş▀╚ř├ÔĚĐ┐╬│╠═Ă╝÷úí | │§╚ř | │§╚ř├ÔĚĐ┐╬│╠═Ă╝÷úí |
┐Ă─┐ú║│§Íđ╩řĐž └┤ď┤ú║ ╠Ôđ═ú║
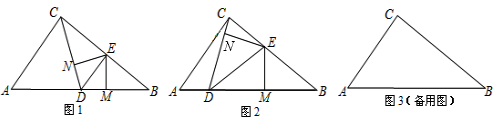
▓Ú┐┤┤░Ş║═ŻÔ╬÷>>
┐Ă─┐ú║│§Íđ╩řĐž └┤ď┤ú║ ╠Ôđ═ú║
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| OC2 |
| 1 |
| OD2 |
| 1 |
| OM2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

▓Ú┐┤┤░Ş║═ŻÔ╬÷>>
┐Ă─┐ú║│§Íđ╩řĐž └┤ď┤ú║ ╠Ôđ═ú║
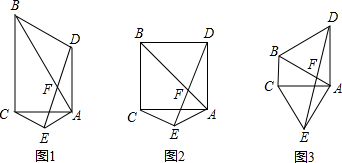
▓Ú┐┤┤░Ş║═ŻÔ╬÷>>
┐Ă─┐ú║│§Íđ╩řĐž └┤ď┤ú║ ╠Ôđ═ú║
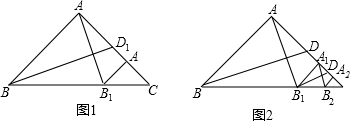
▓Ú┐┤┤░Ş║═ŻÔ╬÷>>
╣˙╝╩ĐžđúË┼Đí - ┴̤░▓ß┴đ▒Ý - ╩ď╠Ô┴đ▒Ý
║■▒▒╩í╗ą┴¬═°╬ąĚĘ║═▓╗┴╝đ┼¤óż┘▒ĘĂŻ╠Ę | ═°╔¤Ëđ║Žđ┼¤óż┘▒ĘÎĘă° | Ášđ┼ŇęĂşż┘▒ĘÎĘă° | ╔Š└˙╩ĚđÚ╬Ů͸ĎňËđ║Žđ┼¤óż┘▒ĘÎĘă° | ╔ŠĂˇăÍ╚Ęż┘▒ĘÎĘă°
╬ąĚĘ║═▓╗┴╝đ┼¤óż┘▒ĘÁš╗░ú║027-86699610 ż┘▒ĘË╩¤ńú║58377363@163.com