练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

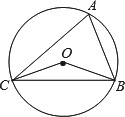
    如图，已知∠OCB＝20°，则∠A＝________度．

    答案：70
    解析：

    　　分析：由OB＝OC与∠OCB＝20°，根据等边对等角，即可求得∠OBC，又由三角形内角和定理，求得∠BOC的度数，然后利用圆周角定理，即可求得∠A的度数．

    　　解答：解：∵OC＝OB，

    　　∴∠OBC＝∠OCB＝20°，

    　　∴∠BOC＝180°－∠OCB－∠OBC＝180°－20°－20°＝140°，

    　　∴∠A＝∠BOC＝70°．

    　　故答案为：70．

    　　点评：此题考查了圆周角定理、等腰三角形的性质以及三角形内角和定理．此题比较简单，注意数形结合思想的应用，注意在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．


    提示：

    考点：圆周角定理．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市密云县2011年中考一模数学试题 题型：044

    已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A(－2，0)，与反比例函数在第一象限内的图象交于点B(2，n)，连接BO，若S△AOB＝4．

    (1)求该反比例函数的解析式和直线AB的解析式；

    (2)若直线AB与y轴的交点为C，求△OCB的面积．

    查看答案和解析>>

    科目：初中数学 来源：2006年湖北省武汉市中考数学试题 题型：013

    已知：如图，AB＝BC，∠ABC＝90°，以AB为直径的⊙O交OC与点D，AD的延长线交BC于点E，过D作⊙O的切线交BC于点F．下列结论：

    ①CD2＝CE·CB；

    ②4EF2＝ED·EA；

    ③∠OCB＝∠EAB；

    ④DF＝CD．其中正确的有

    [　　]

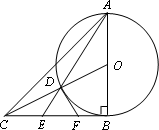
    A．①②③

    B．②③④

    C．①③④

    D．①②④

    查看答案和解析>>

    科目：初中数学 来源：2013年贵州省安顺高级中等学校招生考试数学 题型：044

    已知∶如图，在平面直角坐标系xOy中，直线AB与x轴交于点A(－2，0)，与反比例函数在第一象限内的图象的交于点B(2，n)，连接BO，若S△AOB＝4．

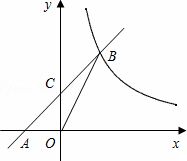
    (1)求该反比例函数的解析式和直线AB的解析式；

    (2)若直线AB与y轴的交点为C，求△OCB的面积．

    查看答案和解析>>

    科目：初中数学 来源：四川省资阳市2011年高中阶段教育学校招生考试数学试卷 题型：044

    在一次机器人测试中，要求机器人从A出发到达B处．如图，已知点A在O的正西方600 cm处，B在O的正北方300 cm处，且机器人在射线AO及其右侧(AO下方)区域的速度为20 cm/秒，在射线AO的左侧(AO上方)区域的速度为10 cm/秒．

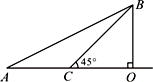
    (1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒)；

    (2)若∠OCB＝45°，求机器人沿A→C→B路线到达B处所用的时间(精确到秒)；

    (3)如图，作∠OAD＝30°，再作BE⊥AD于E，交OA于P．试说明：从A出发到达B处，机器人沿A→P→B路线行进所用时间最短．

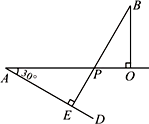
    (参考数据：≈1.414，≈1.732，≈2.236，≈2.449)

    查看答案和解析>>

    同步练习册答案