
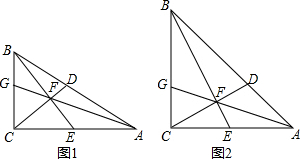
分析 (1)利用中点得出EC=BC,再根据等腰直角三角形的性质得出BF=EF,即可得出BG=DG,再利用三角形的中位线得出AG=DG,即可得出结论;
(2)先利用勾股定理得出BE,再利用三角形的面积公式即可得出CF,然后利用相似三角形的性质得出EF,同理即可得出PE,PE,进而得出AP,最后利用相似三角形的性质即可得出CG,结论得证;
(3)先在Rt△PEF中,用含30°角的直角三角形的性质得出PF,EF,同样的方法在Rt△CEF中,得出CF,CP,进而得出BC,另为利用中点,线段的和差得出AC,AP,最后利用相似三角形的性质得出CG,结论得证.
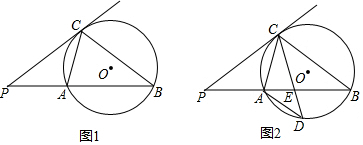
解答 解:(1)如图1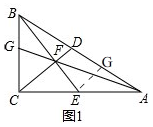 ,∵点E为AC的中点,
,∵点E为AC的中点,
∴EC=BC,
∵∠CEB=∠CBE=45°,
∵CD⊥BE,
∴∠ECF=∠BCF=45°,
∴EF=CF=BF,
作EG∥CD,交AC于G,
∵BF=EF,
∴BD=GD;
∵AE=EC,
∴AG=GD,
∴AG=GD=BD
∴AD=AG+GD=2BD.
(2)如图2,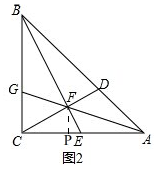 过点F作FP⊥AC于P,
过点F作FP⊥AC于P,
设AE=CE=x,
∴BC=AC=2x,
在Rt△BCE中,根据勾股定理得,BE=$\sqrt{5}$x,
根据△BCE的面积得,$\frac{1}{2}$BC•CE=$\frac{1}{2}$BE•CF,
∴2x•x=$\sqrt{5}$x•CF,
∴CF=$\frac{2\sqrt{5}}{5}x$,
∵BE⊥CD,
∴∠ECF+∠CEF=90°,
∵∠CEF+∠CBE=90°,
∴∠ECF=∠CBE,
∵∠CFE=∠BCE,
∴△CFE∽△BCE,
∴$\frac{EF}{CE}=\frac{CE}{BE}$,
∴$\frac{EF}{x}=\frac{x}{\sqrt{5}x}$,
∴EF=$\frac{\sqrt{5}}{5}$x,
在Rt△CEF中,FP⊥CE,同理可得,PF=$\frac{2}{5}$x,PE=$\frac{1}{5}$x,
∴AP=AE+PE=x+$\frac{1}{5}$x=$\frac{6}{5}$x,
∵FP∥BC,
∴△APF∽△ACG,
∴$\frac{PF}{CG}=\frac{AP}{AC}$,
∴$\frac{\frac{2}{5}x}{CG}=\frac{\frac{6}{5}x}{2x}$,
∴CG=$\frac{2}{3}$x,
∴$\frac{CG}{AC}=\frac{\frac{2}{3}x}{2x}$=$\frac{1}{3}$;
(3)如图2,过点F作FP⊥AC,
∵∠ACD=30°,
∴∠CEF=90°-30°=60°,
在Rt△PEF中,∠EFP=90°-60°=30°,
设PE=a,
在Rt△PEF中,EF=2PE=2a,PF=$\sqrt{3}$PE=$\sqrt{3}$a,
在Rt△CPF中,CF=2PF=2$\sqrt{3}$a,CP=$\sqrt{3}$PF=3a,
∴CE=CP+PE=4a,
∴AC=2CE=8a,
∴AP=AC-CP=5a,
∵FP∥BC,
∴△APF∽△AGC,
∴$\frac{AP}{AC}=\frac{PF}{CG}$,
∴$\frac{5a}{8a}=\frac{\sqrt{3}a}{CG}$,
∴CG=$\frac{8\sqrt{3}}{5}$a,
在Rt△BFC中,∠BCF=90°-∠ACD=60°,
∴∠CBF=30°,
∵CF=2$\sqrt{3}$a,
∴BC=2CF=4$\sqrt{3}$a,
∴BG=BC-CG=4$\sqrt{3}$a-$\frac{8\sqrt{3}}{5}$a=$\frac{12\sqrt{3}}{5}$a,
∴$\frac{BG}{GC}=\frac{\frac{12\sqrt{3}}{5}a}{\frac{8\sqrt{3}}{5}a}$=$\frac{3}{2}$,
故答案为$\frac{3}{2}$.
点评 此题是相似三角形综合题,主要考查了等腰直角三角形的性质,三角形的中位线,勾股定理,相似三角形的判定和性质,含30度角的直角三角形的性质,解(1)关键是判断出BF=EF,解(2)的关键是作出辅助线,利用勾股定理表示出相关线段(CF、EF、PF、PE、AP),解(3)的关键是利用含30度的直角三角形表示相关线段(EF、PF、CF、CE、CP、CE、AC、BC).


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
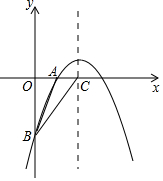 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com