

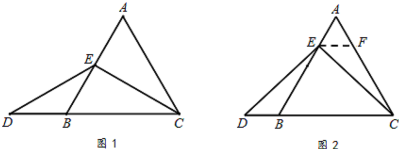
 �۵���EΪAB���е�ʱ����ͼ1 ��ȷ���߶�AE��DB�Ĵ�С��ϵ������ֱ��д�����ۣ�AE( )DB �����������������=������
�۵���EΪAB���е�ʱ����ͼ1 ��ȷ���߶�AE��DB�Ĵ�С��ϵ������ֱ��д�����ۣ�AE( )DB �����������������=������ ��������������=�������������£���ͼ2������E��EF��BC����AC�ڵ�F��������������½����̣�
��������������=�������������£���ͼ2������E��EF��BC����AC�ڵ�F��������������½����̣�|
�⣺��1����Ϊ��=�� |
    |


 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
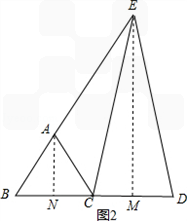
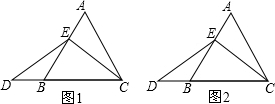 ��2013•����һģ��ij����ѧ���ϣ���ʦ��ʾ��һ���⣬��ͼ1���ڱ߳�Ϊ4�ȱ�������ABC�У���E��AB�ϣ�
��2013•����һģ��ij����ѧ���ϣ���ʦ��ʾ��һ���⣬��ͼ1���ڱ߳�Ϊ4�ȱ�������ABC�У���E��AB�ϣ�| AE |
| AB |
| 1 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| AE |
| AB |
| 1 |
| n |
| mn+m |
| n |
| mn+m |
| n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 420 |
| x |
| 420 |
| x-0.5 |
| 420 |
| x-0.5 |
| 420 |
| x |
| 420 |
| x |
| 420 |
| x-20 |
| 420 |
| x-20 |
| 420 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������8�֣���ѧ���ϣ���ʦ��ʾ�����¿��е���Ŀ��
С����ͬ��С�����ۺ��������½��
��1���������•̽������
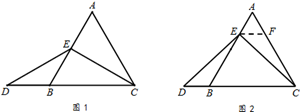
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE���DB��С��ϵ������ֱ��д�����ۣ�
AE DB�����������������=������
��2�����������������Ŀ
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AE DB�����������������=������
�������£���ͼ2������E��EF��BC����AC�ڵ�F.������������½����̣�
��3����չ���ۣ��������
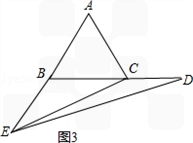
�ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC������ABC��
�߳�Ϊ1��AE=2����CD�ij�������ֱ��д������� ��
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������ʵ��ѧУ2011-2012ѧ����꼶��ѧ����ĩ������ѧ�� ���ͣ������
������8�֣���ѧ���ϣ���ʦ��ʾ�����¿��е���Ŀ��
С����ͬ��С�����ۺ��������½��
��1���������•̽������
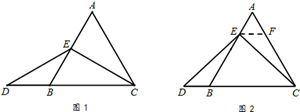
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE���DB��С��ϵ������ֱ��д�����ۣ�
AE DB�����������������=������
��2�����������������Ŀ
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AE DB���� ����������������=������
�������£���ͼ2������E��EF��BC����AC�ڵ�F.������������½����̣�
��3����չ���ۣ��������
�ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC������ABC��
�߳�Ϊ1��AE=2����CD�ij�������ֱ��д������� ��
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ2013����꼶��ѧ����ĩ������ѧ�� ���ͣ�ѡ����
������8�֣���ѧ���ϣ���ʦ��ʾ�����¿��е���Ŀ��
С����ͬ��С�����ۺ��������½��
��1���������•̽������
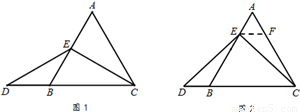
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE���DB��С��ϵ������ֱ��д�����ۣ�
AE DB�����������������=������
��2�����������������Ŀ
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AE DB���� ����������������=������
�������£���ͼ2������E��EF��BC����AC�ڵ�F.������������½����̣�
��3����չ���ۣ��������
�ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC������ABC��
�߳�Ϊ1��AE=2����CD�ij�������ֱ��д������� ��
 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com