
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | 6 |
| X(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
分析 (1)利用网格中数据直接得出乒乓球达到最大高度时的时间;
(2)首先求出函数解析式,进而求出乒乓球落在桌面时,与端点A的水平距离;
(3)①由(2)得乒乓球落在桌面上时,得出对应点坐标,只要利用待定系数法求出函数解析式即可;
②由题意可得,扣杀路线在直线y=$\frac{1}{10}$x上,由①得,y=a(x-3)2-$\frac{1}{4}$a,进而利用根的判别式求出a的值,进而求出x的值.
解答 解:(1)由表格中数据可得,t=0.4(秒),乒乓球达到最大高度;
(2)由表格中数据,可得y是x的二次函数,可设y=a(x-1)2+0.45,
将(0,0.25)代入,可得:a=-$\frac{1}{5}$,
则y=-$\frac{1}{5}$(x-1)2+0.45,
当y=0时,0=-$\frac{1}{5}$(x-1)2+0.45,
解得:x1=$\frac{5}{2}$,x2=-$\frac{1}{2}$(舍去),
即乒乓球与端点A的水平距离是$\frac{5}{2}$m;
(3)①由(2)得乒乓球落在桌面上时,对应点为:($\frac{5}{2}$,0),
代入y=a(x-3)2+k,得($\frac{5}{2}$-3)2a+k=0,
化简得:k=-$\frac{1}{4}$a;
②∵球网高度为0.14米,球桌长(1.4×2)米,
∴扣杀路线在直线经过(0,0)和(1.4,0.14)点,
由题意可得,扣杀路线在直线y=$\frac{1}{10}$x上,由①得,y=a(x-3)2-$\frac{1}{4}$a,
令a(x-3)2-$\frac{1}{4}$a=$\frac{1}{10}$x,
整理得:20ax2-(120a+2)x+175a=0,
当△=(120a+2)2-4×20a×175a=0时符合题意,
解方程得:a1=$\frac{-6+\sqrt{35}}{10}$,a2=$\frac{-6-\sqrt{35}}{10}$,
当a1=$\frac{-6+\sqrt{35}}{10}$时,求得x=-$\frac{\sqrt{35}}{2}$,不符合题意,舍去;
当a2=$\frac{-6-\sqrt{35}}{10}$时,求得x=$\frac{\sqrt{35}}{2}$,符合题意.
点评 此题主要考查了二次函数对应用以及根的判别式和一元二次方程的解法等知识,利用图表中数据得出函数解析式是解题关键.


科目:初中数学 来源: 题型:解答题
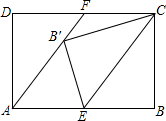 如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.
如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
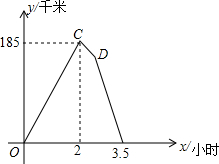 下面的图象反映的过程是:
下面的图象反映的过程是:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
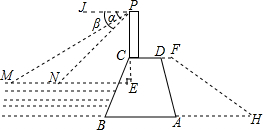 某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我省中学生的视力情况 | |
| B. | 了解九(1)班学生校服的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查台州《600全民新闻》栏目的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com