
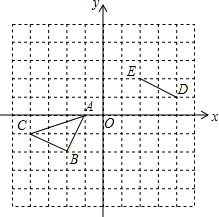
 如图所示的正方形网格中,△ABC的顶点均在格点上,线段DE的两个端点也在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,线段DE的两个端点也在格点上,在所给直角坐标系中解答下列问题:分析 (1)根据平移变换的性质即可求解;
(2)连结BE,CD,确定旋转中心P,再根据旋转变换的性质得到A的对应点F,顺次连结即可求解;
(3)根据扇形的面积计算公式可求出线段AC在旋转过程中扫过的面积.
解答 解:(1)线段DE向下平移3个单位,向左平移6个单位,其与边BC重合;
(2)如图所示: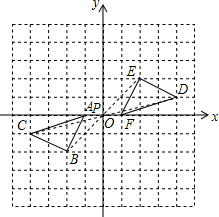
△FED即为所求,P点的坐标为(0,0);
(3)线段AC在旋转过程中扫过的面积为=
线段AB扫过的面积=以0C为半径的扇形的面积-以OA为半径的扇形的面积,
故AC扫过的面积为:$\frac{180π×({1}^{2}+{4}^{2})}{360}$-$\frac{180π×{1}^{2}}{360}$=8π.
故答案为:8π.
点评 此题考查了旋转作图的知识,解答此类题目要明确平移及旋转的特点,另外在第(3)问计算面积的时候要仔细观察图形,将所求面积转化后再求解.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
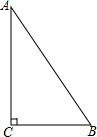 已知,如图所示,在Rt△ABC中,∠C=90°,
已知,如图所示,在Rt△ABC中,∠C=90°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
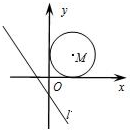 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )| A. | 2.5 | B. | 5-2$\sqrt{2}$ | C. | 2.5或10 | D. | 5-2$\sqrt{2}$或5+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
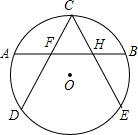 如图所示,CD,CE是⊙O的两条弦,A,B分别是$\widehat{CD}$和$\widehat{CE}$的中点,连接AB交CD于点F,交CE于点H,求证:CF=CH.
如图所示,CD,CE是⊙O的两条弦,A,B分别是$\widehat{CD}$和$\widehat{CE}$的中点,连接AB交CD于点F,交CE于点H,求证:CF=CH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 电视机型号 | A型 | B型 | C型 |
| 销售量(台) | 5 | 10 | 20 |
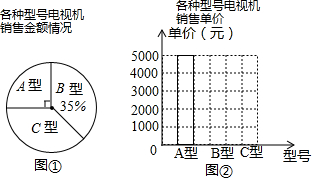
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
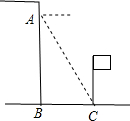 小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)
小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个锐角的补角一定是钝角 | |
| B. | 同角或等角的余角相等 | |
| C. | 两点间的距离是连结这两点的线段的长度 | |
| D. | 过直线l上的一点有且只有一条直线垂直于l |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com