
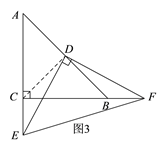
【题目】已知在Rt△ABC中,AC=BC,∠C=90°,点D为AB边的中点,∠EDF=90°,△EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.当∠EDF绕点D旋转到DE⊥AC于点E时(如图①),易证S△DEF+S△CEF=![]() S△ABC.
S△ABC.
当∠EDF绕点D旋转到DE和AC不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的数量关系?请写出你的猜想,不需证明.

【答案】在题中图②的情况下成立.证明见解析;在题中图③情况下不成立,S△DEF,S△CEF,S△ABC的关系是S△DEF-S△CEF=![]() S△ABC.
S△ABC.
【解析】试题分析:
(1)如图,在图②中过点D作DM⊥AC于点M,DN⊥BC于点N,证△DME≌△DNF即可知在图②中,图①中的结论仍然成立;
(2)如图,在图③中,连接CD,证△DCE≌△DBF即可得到S△DEF-S△CEF=![]() S△ABC,由此可知图③中,图①中的结论不在成立,新的关系是:S△DEF-S△CEF=
S△ABC,由此可知图③中,图①中的结论不在成立,新的关系是:S△DEF-S△CEF=![]() S△ABC;
S△ABC;
试题解析:
(1)在图②中,S△DEF+S△CEF=![]() S△ABC.这一结论仍然成立,理由如下:
S△ABC.这一结论仍然成立,理由如下:
过点D作DM⊥AC于点M,DN⊥BC于点N,连接CD,
∴∠DME=∠DNF=90°,
又∵∠C=90°,
∴∠MDN=360°-90°-90°-90°=90°,
又∵∠EDF=90°,
∴∠MDE+∠EDN=∠EDN+∠NDF=90°,
∴∠MDE=∠NDF,
∵△ABC中,∠ACB=90°,点D是AB的中点,AC=BC,
∴CD=AD=BD,∠ADC=∠BDC=90°,
∵DM⊥AC于点M,DN⊥BC于点N,
∴DM=![]() AC,DN=
AC,DN=![]() BC,
BC,
∴DM=DN,
∴△DME≌△DNF,
∴S四边形DMCN=S四边形DECF=S△DEF+S△CEF,
∵由①中结论可知,S△DEF+S△CEF=![]() S△ABC,
S△ABC,
∴在图②中,①中结论仍然成立;

(2)在图③中,①中结论不在成立,此时S△DEF-S△CEF=![]() S△ABC,理由如下:
S△ABC,理由如下:
如图③,连接CD,
∵在△ABC中,∠ACB=90°,点D为AB中点,AC=BC,
∴CD=BD,∠CDB=90°,∠ACD=∠ABC=45°,
∵∠EDF=90°,
∴∠CDE+∠EDB=∠EDB+∠BDF,
∴∠CDE=∠BDF,
∴△DCE≌△DBF,
∴S△DEF=S△DBF+S四边形DBFE
=S△DEC+S四边形DBFE
=S五边形DBFEC
=S△CEF+S△DBC
=S△CEF+S△DBC
=S△CEF+![]() S△ABC,
S△ABC,
∴S△DEF-S△CEF=![]() S△ABC,
S△ABC,
∴图③中,图①中的结论不在成立,新的结论是:S△DEF-S△CEF=![]() S△ABC.
S△ABC.


科目:初中数学 来源: 题型:
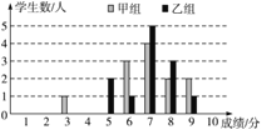
【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题. 
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点o出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位:厘米)依次为 ![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 通过计算说明小虫是否回到起点?如果小虫爬行的速度0.5厘米/秒,小虫共爬行了多少时间?
通过计算说明小虫是否回到起点?如果小虫爬行的速度0.5厘米/秒,小虫共爬行了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点O按顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com