
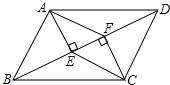
【题目】如图,在□ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断:
(1)△ABE和△CDF全等吗?请说明理由;
(2)四边形AECF是不是平行四边形,并说明理由.
【答案】见解析
【解析】分析:(1)根据平行四边形的性质,可得AB与CD的关系,根据平行线的性质,可得∠ABE=∠CDF,根据AAS,可得答案;
(2)根据平行线的判定,可得AE与CF的关系,根据全等三角形的判定与性质,可得AE与CF的大小关系,根据平行四边形的判定,可得答案.
详解:(1)△ABE≌△CDF,理由如下:
∵在平行四边形ABCD中
∴AB//CD且AB=CD,∠ABE=∠CDF
∵AE⊥BD于E,CF⊥BD于F
∴∠AEB=∠CFD=90°
∴在△ABE和△CDF中,∠AEB=∠CFD,∠ABE=∠CDF,AB=CD
∴△ABE≌△CDF
四边形AECF是平行四边形.理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°,
∴AE∥CF(内错角相等,两直线平行),
由(1)已证△ABE≌△CDF,∴AE=CF,
∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形).


科目:初中数学 来源: 题型:
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果第一天以2元/斤的价格卖出a斤,第二天以1.5元/斤的价格卖出b斤第三天以1.2元/斤的价格卖出c斤,求:
(1)这三天一共卖出水果多少斤?
(2)这三天一共卖得多少钱?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.
(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?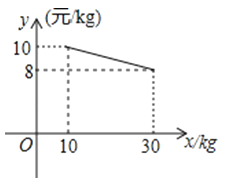
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() ,
, ![]() ,点P为双曲线
,点P为双曲线 ![]() 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 ![]() 于D、C两点,则△PCD的面积为 .
于D、C两点,则△PCD的面积为 . 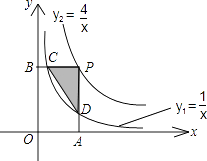
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是___个单位长度;△AOC与△BOD关于直线对称,则对称轴是___;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___度;
(2)连结AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com