
【题目】某校为美化校园,计划对面积为1800平方米区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400平方米区域绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
【答案】解:设乙工程队每天能完成绿化面积是x平方米,则甲工程队每天能完成绿化面积是2x平方米, 根据题意得: ![]() ﹣
﹣ ![]() =4,
=4,
解得:x=50,
经检验,x=50是原方程的解,
∴2x=100.
答:甲、乙两工程队每天能完成绿化的面积分别是100平方米、50平方米
【解析】设乙工程队每天能完成绿化面积是x平方米,则甲工程队每天能完成绿化面积是2x平方米,根据时间=工作总量÷工作效率结合“在独立完成面积为400平方米区域绿化时,甲队比乙队少用4天”,即可得出关于x的分式方程,解之经检验后即可得出结论.
【考点精析】利用分式方程的应用对题目进行判断即可得到答案,需要熟知列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


科目:初中数学 来源: 题型:
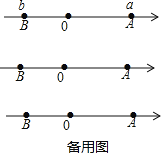
【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足![]() .
.
![]() 写出a、b及AB的距离:
写出a、b及AB的距离:
![]() ______
______ ![]() ______
______ ![]() ______
______
![]() 若动点P从点A出发,以每秒6个单位长度沿数轴向左匀速运动,动点Q从点B出发,以每秒4个单位长度向左匀速运动.
若动点P从点A出发,以每秒6个单位长度沿数轴向左匀速运动,动点Q从点B出发,以每秒4个单位长度向左匀速运动.
![]() 若P、Q同时出发,问点P运动多少秒追上点Q?
若P、Q同时出发,问点P运动多少秒追上点Q?
![]() 若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() 的图象经过点(2,3),下列说法正确的是( )
的图象经过点(2,3),下列说法正确的是( )
A.y随x的增大而增大
B.函数的图象只在第一象限
C.当x<0时,必有y<0
D.点(﹣2,﹣3)不在此函数图象上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD内两点M、N,满足MB⊥BC,MD⊥DC,NB⊥BA,ND⊥DA,若四边形BMDN的面积是菱形ABCD面积的![]() ,则cosA= ______ .
,则cosA= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
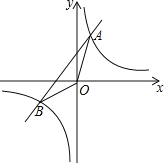
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com