练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．已知x=$\sqrt{5}$+1，求代数式x2-2x-4的值．

    分析 先对所求式子化简，然后将x的值代入即可解答本题．

    解答 解：∵x=$\sqrt{5}$+1，
    ∴x2-2x-4
    =（x-1）2-5
    =$（\sqrt{5}+1-1）^{2}-5$
    =5-5
    =0．

    点评 本题考查二次根式的化简求值，解答本题的关键是明确二次根式化简求值的方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．下列说法中不正确的是（　　）
    A．选举中，人们通常最关心的数据是众数
    B．从1，2，3，4，5中随机抽取一个数，取得奇数的可能性比较大
    C．数据甲、乙的方差分别为S甲2=0.4，S乙2=0.6，则数据甲的波动小
    D．数据3，5，4，1，-2的中位数是4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

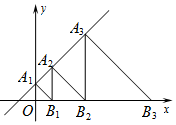    17．如图，直线l：y=x+1交y轴于点A1，在x轴正方向上取点B1，使OB1=OA1；过点B1作A2B1⊥x轴，交l于点A2，在x轴正方向上取点B2，使B1B2=B1A2；过点B2作A3B2⊥x轴，交l于点A3，在x轴正方向上取点B3，使B2B3=B2A3；…记△OA1B1面积为S1，△B1A2B2面积为S2，△B2A3B3面积为S3，…则S2017等于（　　）
    A．24030B．24031C．24032D．24033

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．若-2amb4与5an+2b2m+n是同类项，则mn的值是（　　）
    A．2B．0C．-1D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列根式中能与$\sqrt{3}$合并的二次根式为（　　）
    A．$\sqrt{\frac{3}{2}}$B．$\sqrt{24}$C．$\sqrt{12}$D．$\sqrt{0.5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

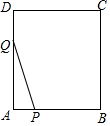    3．如图，长方形ABCD中，AB=10cm，AD=12cn，∠A=90°，点P从点A开始沿着AB边以5cm/s的速度移动，同时另一点Q由A点开始以12cm/s的速度沿着AD边移动．设两点的运动时间为t秒．
    （1）若用含t的式子表示PQ，可以表示为13t．
    （2）试求出使△APQ的面积等于长方形ABCD面积的九分之一的t值．
    （3）若Q点到达D点后立刻按照原路原速返回，试求出何时△APQ为等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

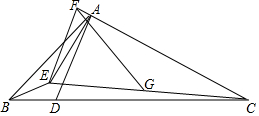    10．在△ABC中，AB=2$\sqrt{6}$，AC=7，AD⊥AC交BC于点D，点E为∠BAD角平分线上一点，连接EA、EB、EC，点G为CE中点，过点E作EF⊥CA交CA延长线于点F，连接FG，若∠EBC=30°，∠AEB=150°，则FG=$\frac{1}{2}$$\sqrt{73}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图①，在锐角△ABC中，AB=5，tanC=3，BD⊥AC于点D，BD=3，点P从点A出发，以每秒1个单位长度的速度沿AB向终点B运动，过点P作PE∥AC交边BC于点E，以PE为边作Rt△PEF，使∠EPF=90°，点F在点P的下方，且EF∥AB．设△PEF与△ABD重叠部分图形的面积为S（平方单位）（S＞0），点P的运动时间为t（秒）（t＞0）．
    （1）求线段AC的长．
    （2）当△PEF与△ABD重叠部分图形为四边形时，求S与t之间的函数关系式．
    （3）若边EF与边AC交于点Q，连结PQ，如图②．
    ①当PQ将△PEF的面积分成1：2两部分时，求AP的长．
    ②直接写出PQ的垂直平分线经过△ABC的顶点时t的值．

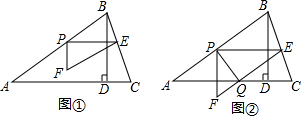
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．定义新运算：对于任意实数a，b都有a⊕b=a（a+b）-2，等式右边是通常的加法、减法及乘法运算，比如：3⊕8=3×（3+8）-2=3×11-2=33-2=31
    （1）求（-2）⊕x=3的值；
    （2）若3⊕x的值小于13，求x的取值范围，并在如图所示的数轴上表示出来．

    查看答案和解析>>

    同步练习册答案