
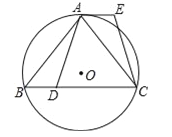
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据等弧所对的圆周角相等,得出∠B=∠ACB,再根据全等三角形的判定得△ABD≌△CAE,即可得出AD=CE;
(2)连接AO并延长,交边BC于点H,由等腰三角形的性质和外心的性质得出AH⊥BC,再由垂径定理得BH=CH,得出CG与AE平行且相等.
试题解析:(1)在⊙O中,∵![]() ,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
(2)连接AO并延长,交边BC于点H,∵![]() ,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.
,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同.
(1)若先从袋子中拿走m个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,则m的值为 ;
(2)若将袋子中的球搅匀后随机摸出1个球(不放回),再从袋中余下的3个球中随机摸出1个球,求两次摸到的球颜色相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)3.587-(-5)+(-5![]() )+(+7)-(+3
)+(+7)-(+3![]() )-(+1.587);
)-(+1.587);
(2)(-1)5×{[-4![]() ÷(-2)2+(-1.25)×(-0.4)]÷(-
÷(-2)2+(-1.25)×(-0.4)]÷(-![]() )-32}.
)-32}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是 ( ).
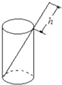
A. 9cm≤h≤10cm B. 10cm≤h≤11cm C. 12cm≤h≤13cm D. 8cm≤h≤9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(2,-3)关于原点对称的点的坐标是( )
A. (2, 3)B. (2, -3)C. (-2,3)D. (-2, -3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
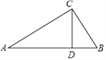
(1)斜边AB的长;
(2)△ABC的面积;
(3)高CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形, ![]() 在同一条直线上,连结
在同一条直线上,连结![]() .
.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索研究.请解决下列问题:
(1)已知△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,并把所有不同的分割方法都画出来,图不够可以自己画.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知等腰△ABC中,AB=AC,D为BC上一点,连接AD,若△ABD和△ACD都是等腰三角形,则∠B的度数为 (请画出示意图,并标明必要的角度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com