
����Ŀ����ͼ������������ʦij�հ�����һ��������̣��������Ӽ���ɢ���ߵ����У��ڳ���ͣ����һ�����������ȥ��꣬����һ����飬Ȼ��첽�ؼң�ͼ���е�ƽ��ֱ������ϵ��x��ʾʱ�䣬y��ʾ����ʦ��ҵľ��룬���������ж����ͼ����ͼ���ṩ����Ϣ������˵���������( )

A. ����ʦ�Ҿ೬��1.5ǧ��
B. ����ʦ�����ͣ����30����
C. ����ʦ�Ӽ��ﵽ���е�ƽ���ٶ���ӳ��е�����ƽ���ٶ�����ȵ�
D. ����ʦ����굽�ҵ�ƽ���ٶ���10ǧ�ף�ʱ
���𰸡�D
��������
����ͼ���е�������Ϣ���з����жϼ���.
Aѡ���У���ͼ���֪��������ʦ�Ҿ��볬��1.5km��������A��˵����ȷ��
Bѡ���У���ͼ���֪������ʦ�����ͣ����ʱ��Ϊ��80-50=30�����ӣ�������B��˵����ȷ��
Cѡ���У���ͼ���֪������ʦ�Ӽ��ﵽ���е�ƽ���ٶ�Ϊ��1500��30=50����/���ӣ�������ʦ�ӳ��е�����ƽ���ٶ�Ϊ����2000-1500���£�50-40��=50����/���ӣ�������C��˵����ȷ��
Dѡ���У���ͼ���֪������ʦ����굽�ҵ�ƽ���ٶ�Ϊ��2000�£�100-80��=100����/���ӣ�=6��ǧ��/ʱ��������D��˵������.
��ѡD.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y=��x2+3��x��Χ�ɷ�����߽���⣩�����㣨��ĺᡢ�����궼���������ĸ���Ϊk����������y= ![]() ��x��0����ͼ���ǣ� ��
��x��0����ͼ���ǣ� �� 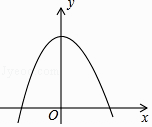
A.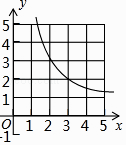
B.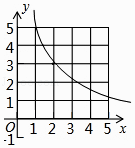
C.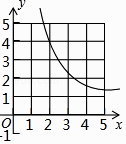
D.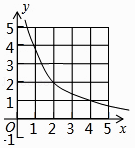
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������У�����������ִ������������в����ݳ����ɼ�����ѡ��![]() ��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ������ÿ����
��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ������ÿ����![]() ��ѡ�ֵľ����ɼ���ͼ��ʾ��
��ѡ�ֵľ����ɼ���ͼ��ʾ��

![]() �����
�����
ƽ�������֣� | ��λ�����֣� | �������֣� | |
������� |
|
| |
������� |
|
|
![]() ������Ӿ����ɼ���ƽ��������λ���������ĸ������ӵijɼ��Ϻã�
������Ӿ����ɼ���ƽ��������λ���������ĸ������ӵijɼ��Ϻã�
![]() �������Ӿ����ɼ��ķ�����ж��ĸ������ӵijɼ���Ϊ�ȶ���
�������Ӿ����ɼ��ķ�����ж��ĸ������ӵijɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��һ�ι㲥�ٱ����У�������ĸ���÷����±���
��װͳһ | �������� | ����ȷ | |
�ˣ�1���� | 80 | 84 | 87 |
�ˣ�2���� | 97 | 78 | 80 |
�ˣ�3���� | 90 | 78 | 85 |
(1) ��գ����ݱ����ṩ����Ϣ���ڷ�װͳһ���棬������÷ֵ�ƽ������_________���ڶ���ȷ�����������Ƶ���_________��
(2) �����װͳһ���������롢����ȷ�������水20%��30%��50%�ı����������ĵ÷֣���ͨ������˵���ĸ���ĵ÷����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ����45��ǵ�ֱ�����ǰ�ECF��һ��������ABCD�ڷ���һ��ʹ���ǰ��ֱ�Ƕ���������εĶ���C�غϣ���E��F�ֱ��������εı�CB��CD�ϣ�����AF��ȡAF�е�M��EF���е�N������MD��MN��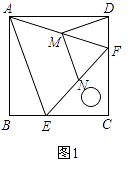
��1������̽����
����1��DM��MN��������ϵ����
����2��DM��MN��λ�ù�ϵ����
��2��������֤��֤����Ľ��ۣ�
��3����չ����ͼ2����ͼ1�е�ֱ�����ǰ�ECF�Ƶ�C˳ʱ����ת180�㣬�����������䣬��1���е��������ۻ��������������������֤����������������˵�����ɣ�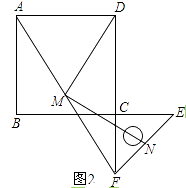
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ȫ��ͬѧ�μ���ij�������������˲���ͬѧ�������ͳ����ͼ��ʾ��
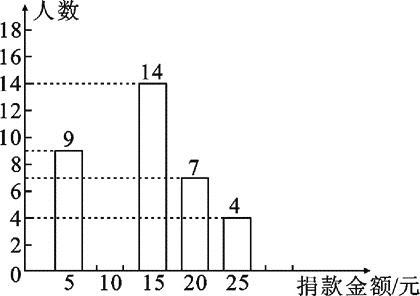
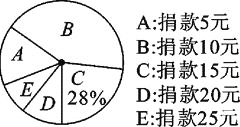
��1�����ι����ѧ��________�ˣ���������ͼ����������
��2��������������________��ƽ������________����λ��Ϊ________��
��3���ڰ��꼶600��ѧ���У����20Ԫ�����ϣ���20Ԫ����ѧ�������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
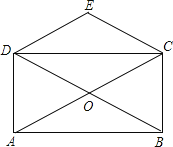
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��CE��BD��DE��AC��
��1��֤�����ı���OCEDΪ���Σ�
��2����AC=4�����ı���CODE���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У������ȵ��ǣ� ��
A.��12�루��1��2
B.![]() ??
??
C.��|��2|�멁����2��
D.����3��3�멁33
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��![]() �ֱ���x�ᡢy�ύ�ڵ�B��C������ֱ��l2��
�ֱ���x�ᡢy�ύ�ڵ�B��C������ֱ��l2��![]() ���ڵ�A��
���ڵ�A��
��1�������A������
��2����D���߶�OA�ϵĵ㣬�ҡ�COD�����Ϊ12����ֱ��CD�Ľ���ʽ
��3���ڣ�2���������£���P������CD�ϵĵ㣬��ƽ�����Ƿ���ڵ�Q��ʹ��O��C��P��QΪ������ı��������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com