
【题目】如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.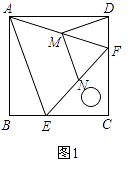
(1)尝试探究:
结论1:DM、MN的数量关系是;
结论2:DM、MN的位置关系是;
(2)猜想论证:证明你的结论.
(3)拓展:如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,(1)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.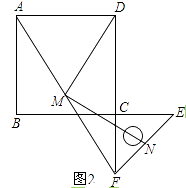
【答案】
(1)DM=MN;DM⊥MN
(2)
解:结论1:DM=MN,理由是:
如图1,∵M是AF的中点,N是EF的中点,
∴MN= ![]() AE,
AE,
∵四边形ABCD是正方形,
∴∠ADF=∠B=90°,AB=AD=BC=CD,
∴DM= ![]() AF,
AF,
∵△ECF是等腰直角三角形,
∴EC=FC,
∴BE=DF,
在△ABE和△ADF中,
∵  ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∴DM=MN;
结论2,DM、MN的位置关系是:DM⊥MN,理由是:
如图1,∵M是AF的中点,N是EF的中点,
∴MN∥AE,
∴∠NMF=∠EAF,
∵△ABE≌△ADF,
∴∠BAE=∠FAD,
Rt△ADF中,∵M是AF的中点,
∴AM=DM,
∴∠FAD=∠MDA,
∵∠FMD=∠FAD+∠MDA=∠FAD+∠BAE,
∴∠DMN=∠NMF+∠FMD=∠EAF+∠BAE+∠FAD=90°,
∴DM⊥MN
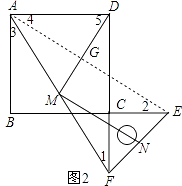
(3)
解:(2)中的两个结论还成立,
证明:连接AE,交MD于点G,
∵点M为AF的中点,点N为EF的中点,
∴MN∥AE,MN= ![]() AE,
AE,
由(1)同理可证,
AB=AD=BC=CD,∠B=∠ADF,CE=CF,
又∵BC+CE=CD+CF,即BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
在Rt△ADF中,
∵点M为AF的中点,
∴DM= ![]() AF,
AF,
∴DM=MN,
∵△ABE≌△ADF,
∴∠1=∠2,
∵AB∥DF,
∴∠1=∠3,
同理可证:∠2=∠4,
∴∠3=∠4,
∵DM=AM,
∴∠MAD=∠5,
∴∠DGE=∠5+∠4=∠MAD+∠3=90°,
∵MN∥AE,
∴∠DMN=∠DGE=90°,
∴DM⊥MN.
【解析】解:(1)结论1:DM、MN的数量关系是:DM=MN,
结论2:DM、MN的位置关系是:DM⊥MN,
所以答案是:DM=MN,DM⊥MN;
【考点精析】本题主要考查了直角三角形斜边上的中线和三角形中位线定理的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】在学校组织的知识竞赛中,八(1)班比赛成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩整理并绘制成如下的统计图.
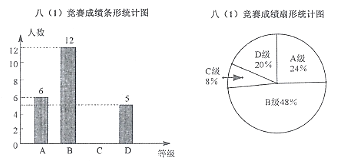
请你根据以上提供的信息解答下列问题:
(1)请根据统计图的信息求出成绩为C等级的人数;
(2)将表格补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= ![]() (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.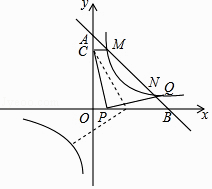
(1)求k2﹣k1的值;
(2)若 ![]() =
= ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
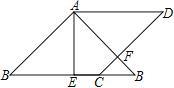
A. 1 B. ![]() C. 2
C. 2![]() -2 D. 2-
-2 D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
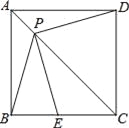
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF. 
(1)求证:△BOE≌△DOF;
(2)若OA= ![]() BD,则四边形ABCD是什么特殊四边形?请说明理由.
BD,则四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com