
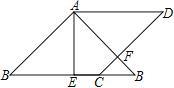
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A. 1 B. ![]() C. 2
C. 2![]() -2 D. 2-
-2 D. 2-![]()
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=kx+b(k<0)与函数y= ![]() (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, ![]() )、(c,
)、(c, ![]() ),其中a>c>0.
),其中a>c>0.
(1)如图①,求证:∠EDP=∠ACP;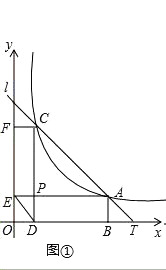
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;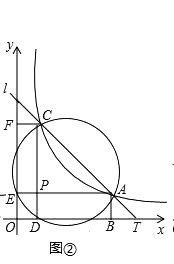
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.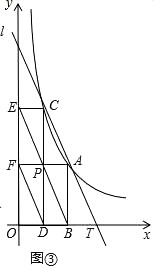
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出![]() 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队![]() 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:

![]() 填表:
填表:
平均数(分) | 中位数(分) | 众数(分) | |
初中代表队 |
|
| |
高中代表队 |
|
|
![]() 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
![]() 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
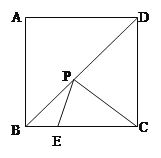
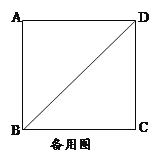
【题目】如图,正方形ABCD的边长为![]() ,点P为对角线BD上一动点,点E在射线BC上,
,点P为对角线BD上一动点,点E在射线BC上,
(1)填空:BD=______;
(2)若BE=t,连结PE、PC,求PE+PC的最小值(用含t的代数式表示);
(3)若点E是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级在一次广播操比赛中,三个班的各项得分如下表:
服装统一 | 动作整齐 | 动作准确 | |
八(1)班 | 80 | 84 | 87 |
八(2)班 | 97 | 78 | 80 |
八(3)班 | 90 | 78 | 85 |
(1) 填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是_________;在动作准确方面最有优势的是_________班
(2) 如果服装统一、动作整齐、动作准确三个方面按20%、30%、50%的比例计算各班的得分,请通过计算说明哪个班的得分最高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.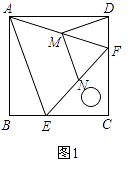
(1)尝试探究:
结论1:DM、MN的数量关系是;
结论2:DM、MN的位置关系是;
(2)猜想论证:证明你的结论.
(3)拓展:如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,(1)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.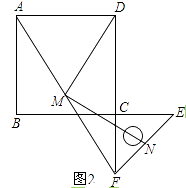
查看答案和解析>>
科目:初中数学 来源: 题型:
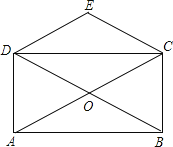
【题目】如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
(1)证明:四边形OCED为菱形;
(2)若AC=4,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com