
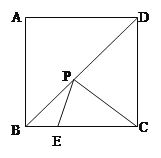
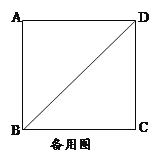
【题目】如图,正方形ABCD的边长为![]() ,点P为对角线BD上一动点,点E在射线BC上,
,点P为对角线BD上一动点,点E在射线BC上,
(1)填空:BD=______;
(2)若BE=t,连结PE、PC,求PE+PC的最小值(用含t的代数式表示);
(3)若点E是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.
【答案】(1)BD=2 (2)![]() (3)120° 30°
(3)120° 30°
【解析】.
(1)根据勾股定理计算即可;
(2)连接AP,当AP与PE在一条线上时,PE+PC最小,利用勾股定理求出最小值;
(3)分两种情况考虑:①当E在BC延长线上时,如图2所示,△PCE为等腰三角形,则CP=CE;②当E在BC上,如图3所示,△PCE是等腰三角形,则PE=CE,分别求出∠PEC的度数即可.
(1)BD=![]() =2 ;
=2 ;
(2)如图1所示:当AP与PE在一条线上时,PE+PC最小,
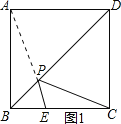
∵AB=![]() ,BE=t,
,BE=t,
∴PE+PC的最小值为![]() ,
,
(3)分两种情况考虑:
①当点E在BC的延长线上时,
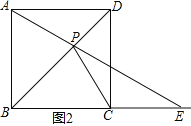
如图2所示,△PCE是等腰三角形,则CP=CE,
∴∠CPE=∠CEP,
∴∠BCP=∠CPE+∠CEP=2∠CEP,
∵在正方形ABCD中,∠ABC=90°,
∴∠PBA=∠PBC=45°,
在△ABP和△CBP中,
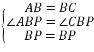 ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=2∠CEP,
∵∠BAP+∠PEC=90°,
∴2∠PEC+∠PEC=90°,
∴∠PEC=30°;
②当点E在BC上时,
如图3所示,△PCE是等腰三角形,则PE=CE,
∴∠CPE=∠PCE,
∴∠BEP=∠CPE+∠PCE=2∠ECP,
∵四边形ABCD是正方形,
∴∠PBA=∠PBC=45°,
又AB=BC,BP=BP,
∴△ABP≌△CBP,
∴∠BAP=∠BCP,
∵∠BAP+∠AEB=90°,
∴2∠BCP+∠BCP=90°,
∴∠BCP=30°,
∴∠AEB=60°,
∴∠PEC=180°-∠AEB=120° .


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
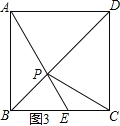
【题目】如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)如图 1,若 CE 恰好是∠ACD 的角平分线,请你猜想此时 CD 是不是∠ECB 的角平分线?只回答出“是”或“不是”即可;
(2)如图 2,若∠ECD=α,CD 在∠BCE 的内部,请你猜想∠ACE 与∠DCB是否相等?并简述理由;
(3)在(2)的条件下,请问∠ECD 与∠ACB 的和是多少?并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) 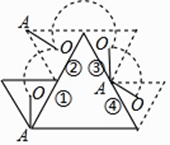
A.240°
B.360°
C.480°
D.540°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= ![]() (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.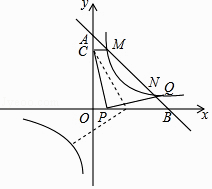
(1)求k2﹣k1的值;
(2)若 ![]() =
= ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
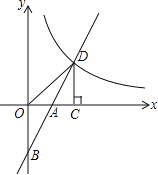
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
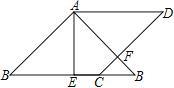
A. 1 B. ![]() C. 2
C. 2![]() -2 D. 2-
-2 D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com