
【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
【答案】①②④
【解析】解:∵抛物线过点A(﹣1,1),B(2,4), ∴ ![]() ,
,
∴b=﹣a+1,c=﹣2a+2.
∵a>0,
∴b<1,c<2,
∴结论①②正确;
∵抛物线的顶点坐标为(m,n),
∴m=﹣ ![]() =﹣
=﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴m< ![]() ,结论③不正确;
,结论③不正确;
∵抛物线y=ax2+bx+c(a>0)经过A(﹣1,1),顶点坐标为(m,n),
∴n≤1,结论④正确.
综上所述:正确的结论有①②④.
所以答案是:①②④.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
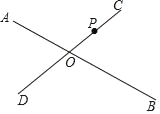
【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的知识竞赛中,八(1)班比赛成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩整理并绘制成如下的统计图.
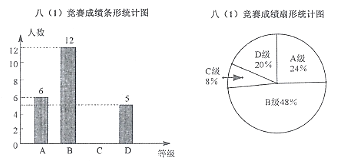
请你根据以上提供的信息解答下列问题:
(1)请根据统计图的信息求出成绩为C等级的人数;
(2)将表格补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线相交于O,给出下列 5个条件:①AB∥CD ;②AD∥BC;③AB=CD ;④∠BAD=∠BCD;⑤OA=OC.从以上5个条件中任选 2个条件为一组,能推出四边形ABCD为平行四边形的有( )
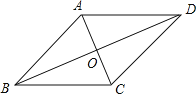
A. 4组 B. 5组 C. 6组 D. 7组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) 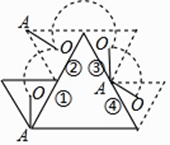
A.240°
B.360°
C.480°
D.540°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)画出数轴,并在数轴上画出表示下列各数的点:﹣4.5,﹣2,3,0,4;
(2)用“<”号将(1)中各数连接起来;
(3)直接填空:数轴上表示3和表示1的两点之间的距离是_____,数轴上A点表示的数为4,B点表示的数为﹣2,则A、B之间的距离是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= ![]() (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.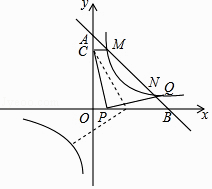
(1)求k2﹣k1的值;
(2)若 ![]() =
= ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
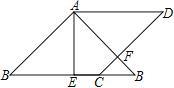
A. 1 B. ![]() C. 2
C. 2![]() -2 D. 2-
-2 D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
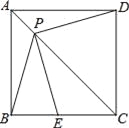
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com