
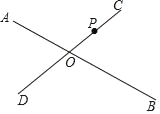
【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】“*”是新规定的这样一种运算法则:a*b=a2+2ab,比如3*(﹣2)=32+2×3×(﹣2)=﹣3
(1)试求2*(﹣3)的值;
(2)若2*x=2,求x的值;
(3)若(﹣2)*(1*x)=x+9,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蚂蚁从点O出发,在一条直线上来回爬行.假定向右爬行的路程记为正数,向左爬行的路程记为负数,则爬过的各段路程依次记为(单位:cm):+5,-3,+10,-8,-6,+12,-10.
![]()
(1)蚂蚁最后是否回到出发点O?
(2)蚂蚁离开出发点O最远是多少?
(3)在爬行过程中,如果每爬行1奖励一粒糖,那么蚂蚁一共得到多少粒糖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ![]() ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 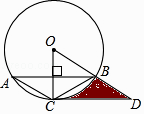
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O. 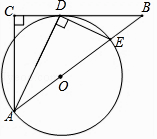
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
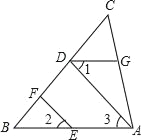
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段 AB 的长为 10cm,C 是直线 AB 上一动点,M 是线段 AC的中点,N 是线段 BC 的中点.
(1)若点 C 恰好为线段 AB 上一点,求MN等于多少cm;
(2)猜想线段 MN 与线段 AB 长度的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=kx+b(k<0)与函数y= ![]() (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, ![]() )、(c,
)、(c, ![]() ),其中a>c>0.
),其中a>c>0.
(1)如图①,求证:∠EDP=∠ACP;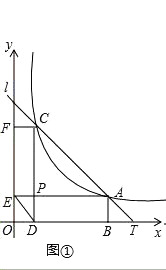
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;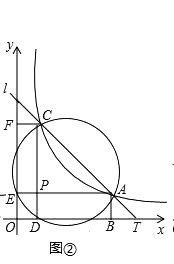
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.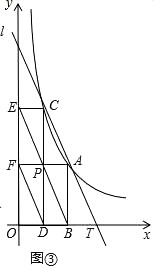
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com