
【题目】蚂蚁从点O出发,在一条直线上来回爬行.假定向右爬行的路程记为正数,向左爬行的路程记为负数,则爬过的各段路程依次记为(单位:cm):+5,-3,+10,-8,-6,+12,-10.
![]()
(1)蚂蚁最后是否回到出发点O?
(2)蚂蚁离开出发点O最远是多少?
(3)在爬行过程中,如果每爬行1奖励一粒糖,那么蚂蚁一共得到多少粒糖?
【答案】(1)回到了出发点;(2)12cm;(3)54粒
【解析】试题分析:(1)要想知道蚂蚁是否能回到原点,关键是看它分别向左向右的爬行路程之和是否为0.
(2)离出发点最远的距离,就是将小虫爬行的路程依次相加,看看走到哪一段是最大值.
(3)要求一共得到多少米粒,即就是问蚂蚁一共爬行了多少路程即可.
解:(1)将所有记录的路程相加,得
(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)
=((+5)+(+10)+(+12))+((-3)+(-8)+(-6)+(-10))
=27+(-27)
=0(cm).
即左右爬行的路程相同, 蚂蚁最后回到出发点O.
(2)根据记录的数据,得
蚂蚁离出发点最远的距离是(+5)+(-3)+(+10)=12(cm).
(3)取所有路程的绝对值,得
|+5|+|3|+|+10|+|8|+|6|+|+12|+|10|
=5+3+10+8+6+12+10
=54(cm).
由于每爬行1cm,奖励一粒糖,所以蚂蚁一共得到芝麻的粒数为:54×1=54(粒).
答: 蚂蚁一共得到54粒糖.


科目:初中数学 来源: 题型:
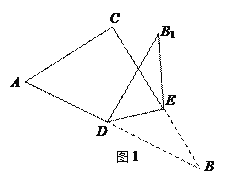
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3,点D为AB的中点,点E为线段BC上的点,连接DE,把△BDE沿着DE翻折得△B1DE.
(1)当A、D、B1、C构成的四边形为平行四边形,求DE的长;
(2)当DB1⊥AC时,求△DE B1和△ABC重叠部分的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
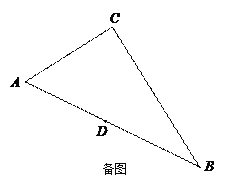
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.
(1)求抛物线的解析式;
(2)用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;
(3)求△BCE的面积最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中数学 来源: 题型:
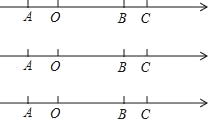
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)判断△BEC的形状,并说明理由?
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;
(3)求四边形EFPH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
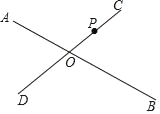
【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的知识竞赛中,八(1)班比赛成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩整理并绘制成如下的统计图.
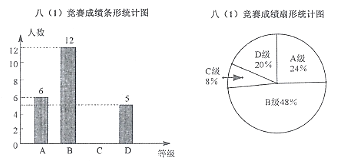
请你根据以上提供的信息解答下列问题:
(1)请根据统计图的信息求出成绩为C等级的人数;
(2)将表格补充完整.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com