
【题目】如图,直线l:y=kx+b(k<0)与函数y= ![]() (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, ![]() )、(c,
)、(c, ![]() ),其中a>c>0.
),其中a>c>0.
(1)如图①,求证:∠EDP=∠ACP;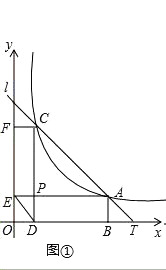
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;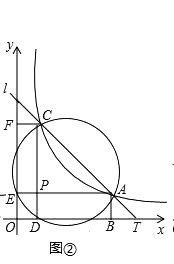
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.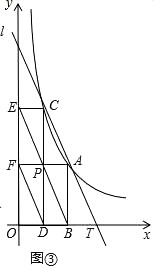
【答案】
(1)
证明:由题意可知P(c, ![]() ),E(0,
),E(0, ![]() ),D(c,0),
),D(c,0),
∴PA=a﹣c,EP=c,PC= ![]() ﹣
﹣ ![]() =
= ![]() ,DP=
,DP= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,且∠EPD=∠APC,
,且∠EPD=∠APC,
∴△EPD∽△CPA,
∴∠EDP=∠ACP
(2)
如图1,连接AD、EC,
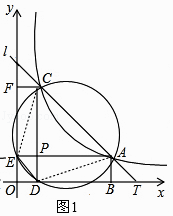
由(1)可知DE//AC,
∴∠DEC+∠ECA=180°,
∵A、D、E、C四点在同圆周上,
∴∠DEC+∠DAC=180°,
∴∠ECA=∠DAC,
在△AEC和△CDA中
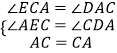
∴△AEC≌△CDA(AAS),
∴CD=AE,即a= ![]() ,可得ac=4,
,可得ac=4,
∵A、C在直线l上,
∴ 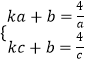 ,解得k=
,解得k= ![]() =﹣
=﹣ ![]() =﹣1
=﹣1
(3)
假设在线段AT上存在点M,使OM⊥AM,连接OM、OA,作MN⊥x轴于点N,如图2,
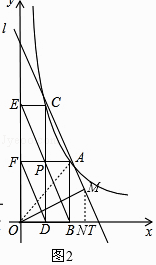
∵c=1,
∴C(1,4),F(0,4),P(1, ![]() ),B(a,0),
),B(a,0),
设直线BF的解析式为y=k′x+4,由题意可得 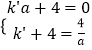 ,解得a=2,
,解得a=2,
∴A(2,2),
∴AP为△DCT的中位线,
∴T(3,0),
∴AT= ![]() =
= ![]()
∵S△OAT= ![]() OTAB=
OTAB= ![]() ATOM,
ATOM,
∴OM= ![]() =
= ![]() =
= ![]() ,
,
在Rt△OMT中,MT= ![]() =
= ![]() =
= ![]() ,
,
同理可求得MN= ![]() =
= ![]() ,
,
在Rt△OMN中,ON= ![]() =
= ![]() =
= ![]() ,
,
∵2< ![]() <3,
<3,
∴点M在线段AT上,
即在线段AT上存在点M,使得OM⊥AM,M点的坐标为( ![]() ,
, ![]() )
)
【解析】(1)由P、E、D的坐标可表示出PA、EP、PC和DP的长,可证明△EPD∽△CPA,利用相似三角形的性质可证得结论;(2)连接AD、EC,可证明△AEC≌△CDA,可得CD=AE,把A、C坐标代入直线l解析式,可求得k的值;(3)假设在线段AT上存在点M,使得OM⊥AM,连接OM、OA,可表示出C、F、P、B的坐标,利用直线BF的解析式可求得a的值,可求得A点坐标,可求得T点坐标,在△OAT中,利用等积法可求得OM的长,在RtOMT中可求得MT的长,作MN⊥x轴,同理可求得MN的长,则可求得ON的长,可判断N在线段BT上,满足条件,从而可知存在满足条件的M点.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.
(1)求抛物线的解析式;
(2)用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;
(3)求△BCE的面积最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
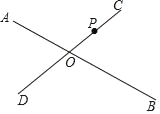
【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角三角形的三边长分别为a、b、c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形。那么,这四个图形中,其面积![]() 满足
满足![]() 的个数是( )
的个数是( )
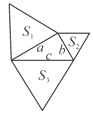
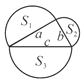
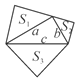

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)如图 1,若 CE 恰好是∠ACD 的角平分线,请你猜想此时 CD 是不是∠ECB 的角平分线?只回答出“是”或“不是”即可;
(2)如图 2,若∠ECD=α,CD 在∠BCE 的内部,请你猜想∠ACE 与∠DCB是否相等?并简述理由;
(3)在(2)的条件下,请问∠ECD 与∠ACB 的和是多少?并简述理由.
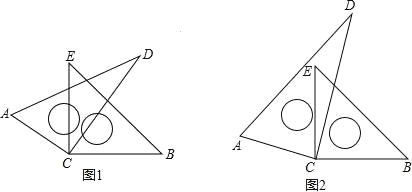
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件正确的是( )
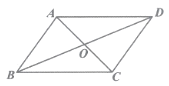
A. AB=AD B. AC=BD C. ∠ABC=90° D. ∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的知识竞赛中,八(1)班比赛成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩整理并绘制成如下的统计图.
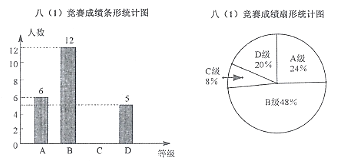
请你根据以上提供的信息解答下列问题:
(1)请根据统计图的信息求出成绩为C等级的人数;
(2)将表格补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线相交于O,给出下列 5个条件:①AB∥CD ;②AD∥BC;③AB=CD ;④∠BAD=∠BCD;⑤OA=OC.从以上5个条件中任选 2个条件为一组,能推出四边形ABCD为平行四边形的有( )
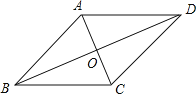
A. 4组 B. 5组 C. 6组 D. 7组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
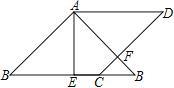
A. 1 B. ![]() C. 2
C. 2![]() -2 D. 2-
-2 D. 2-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com