
【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O. 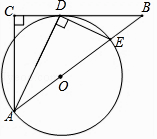
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
【答案】
(1)证明:连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO= ![]() AE,
AE,
∴点D在⊙O上,且∠DAO=∠ADO.
又∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠ADO=∠CAD,
∴AC∥DO.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
又∵OD为半径,
∴BC是⊙O的切线
(2)解:∵在Rt△ACB中,AC=3,BC=4,
∴AB=5.
设OD=r,则BO=5﹣r.
∵OD∥AC,
∴△BDO∽△BCA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:r= ![]() ,
,
∴BE=AB﹣AE=5﹣ ![]() =
= ![]()
【解析】(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;(2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5﹣r,由OD∥AC可得出 ![]() =
= ![]() ,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)判断△BEC的形状,并说明理由?
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;
(3)求四边形EFPH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
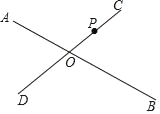
【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)当x=______时,点P到点A,点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是______;
(4)在数轴上,点M,N表示的数分别为x![]() ,x
,x![]() ,我们把x
,我们把x![]() ,x
,x![]() 之差的绝对值叫做点M,N之间的距离,即MN="|" x
之差的绝对值叫做点M,N之间的距离,即MN="|" x![]() -x
-x![]() |.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
|.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
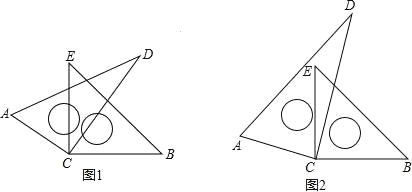
【题目】如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)如图 1,若 CE 恰好是∠ACD 的角平分线,请你猜想此时 CD 是不是∠ECB 的角平分线?只回答出“是”或“不是”即可;
(2)如图 2,若∠ECD=α,CD 在∠BCE 的内部,请你猜想∠ACE 与∠DCB是否相等?并简述理由;
(3)在(2)的条件下,请问∠ECD 与∠ACB 的和是多少?并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) 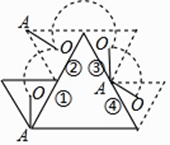
A.240°
B.360°
C.480°
D.540°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com