练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求证：关于x的一元二次方程x2-（2k-1）x-3k-3=0总有两个不同的实数根．

    证明：∵△=[-（2k-1）]2-4×1×（-3k-3）
    =4k2-4k+1+12k+12，
    =4k2+8k+13
    =（2k+2）2+9
    而（2k+2）2≥0，
    ∴△＞0．
    所以方程总有两个不相等的实数根．
    分析：要证明方程有两个不相等的实数根，即证明△＞0即可．
    点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax2-bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．
    （1）若方程①的根为正整数，求整数k的值；
    （2）求代数式
    (kc)2-b2+abakc
    的值；
    （3）求证：关于x的一元二次方程ax2-bx+c=0 ②必有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源：2012年北京市中考数学二模练习试卷（一）（解析版） 题型：解答题

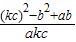    已知：关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax2-bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．
    （1）若方程①的根为正整数，求整数k的值；
    （2）求代数式的值；
    （3）求证：关于x的一元二次方程ax2-bx+c=0 ②必有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源：2009年湖北省荆州市沙市区十四中中考数学仿真试卷（四）（解析版） 题型：解答题

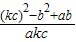    已知：关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax2-bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．
    （1）若方程①的根为正整数，求整数k的值；
    （2）求代数式的值；
    （3）求证：关于x的一元二次方程ax2-bx+c=0 ②必有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源：2009年北京市海淀区中考数学一模试卷（解析版） 题型：解答题

    （2009•海淀区一模）已知：关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax2-bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．
    （1）若方程①的根为正整数，求整数k的值；
    （2）求代数式的值；
    （3）求证：关于x的一元二次方程ax2-bx+c=0 ②必有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012年北京四中九年级第一学期期中考试数学卷 题型：解答题

    已知： 关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax2−bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．

    1.（1）若方程①的根为正整数，求整数k的值；

    2.（2）求代数式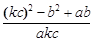的值；

    3.（3）求证： 关于x的一元二次方程ax2−bx+c=0 ②必有两个不相等的实数根．

     

     

    查看答案和解析>>

    同步练习册答案