
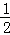 x2+
x2+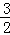 x+2����D������3��2����2��p1��0��2����p2��
x+2����D������3��2����2��p1��0��2����p2�� ����2����p3��
����2����p3��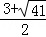 ����2����3����P������
����2����3����P������ ��
��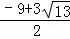 ��������
�������� ��
�� ����
���� ��
��
 x2+
x2+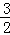 x+2��
x+2��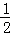 x2+
x2+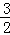 x+2=2����ã�x1=3��x2=0���ᣩ��
x+2=2����ã�x1=3��x2=0���ᣩ��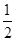 x2+
x2+ 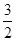 x+2=��2
x+2=��2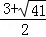 ��x2=
��x2=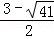 ��
��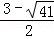 ����2������
����2������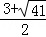 ����2��
����2�� ����2����p3��
����2����p3��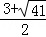 ����2����
����2����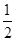 a2+
a2+ 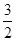 a+2����
a+2����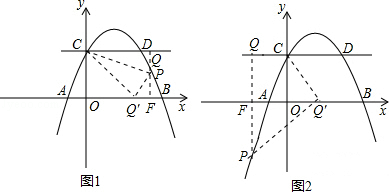
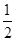 a2+
a2+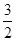 a+2��=
a+2��=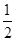 a2��
a2��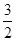 a��
a��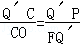 ��
��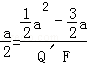 ��
��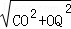 =
=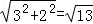 ��
�� ����P��������
����P�������� ��
��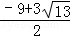 ����
����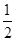 a2+
a2+ 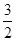 a+2��0��CQ=��a��
a+2��0��CQ=��a��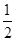 a2+
a2+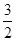 a+2��=
a+2��=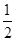 a2��
a2��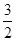 a��
a��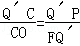 ��
��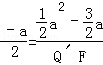 ��Q��F=3��a��
��Q��F=3��a��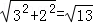 ��
�� ����P����������
����P���������� ��
��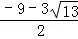 ����
���� ��
�� ��������
�������� ��
�� ����
����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ʱ��y��ֵ��
ʱ��y��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
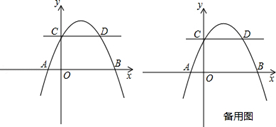
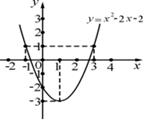
 ��x���ཻ��B��1��0����C��4��0�����㣬��y����������ཻ��A�㣬��A��B��C����ġ�P��y�������ڵ�A��MΪy�Ḻ�����ϵ�һ�����㣬ֱ��MB����P�ڵ�D�����������ڵ�N��
��x���ཻ��B��1��0����C��4��0�����㣬��y����������ཻ��A�㣬��A��B��C����ġ�P��y�������ڵ�A��MΪy�Ḻ�����ϵ�һ�����㣬ֱ��MB����P�ڵ�D�����������ڵ�N��
 ����N�����ꣻ
����N�����ꣻ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
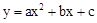 ��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B����Ϊ����1��0������������ĸ����ۣ���2a+b=0����4a��2b��c��0����ac��0���ܵ�y��0ʱ��x����1��x��2��������ȷ�ĸ�����
��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B����Ϊ����1��0������������ĸ����ۣ���2a+b=0����4a��2b��c��0����ac��0���ܵ�y��0ʱ��x����1��x��2��������ȷ�ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ������������y=(b+c)x��ͬһ����ϵ�еĴ���ͼ������ǣ� ��
������������y=(b+c)x��ͬһ����ϵ�еĴ���ͼ������ǣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
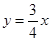 ����A�������ǣ�4��0������DΪx����λ�ڵ�A�ұߵ�ijһ�㣬��BΪֱ��
����A�������ǣ�4��0������DΪx����λ�ڵ�A�ұߵ�ijһ�㣬��BΪֱ��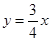 �ϵ�һ�㣬�Ե�A��B��DΪ�����������Σ�
�ϵ�һ�㣬�Ե�A��B��DΪ�����������Σ�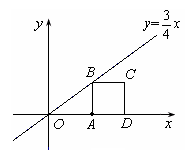
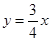 �ӵ�O�ƶ�����B�����ͬʱ��Q����ͬ���ٶȴӵ�A������������A��B��C�ƶ�������P�����Bʱ����ֹͣ�˶�����̽�������ƶ������У���PAQ��������ֵ�Ƕ��٣�
�ӵ�O�ƶ�����B�����ͬʱ��Q����ͬ���ٶȴӵ�A������������A��B��C�ƶ�������P�����Bʱ����ֹͣ�˶�����̽�������ƶ������У���PAQ��������ֵ�Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����ƽ��3����λ��������ƽ��2����λ����ô�õ��������ߵĽ���ʽΪ ��
����ƽ��3����λ��������ƽ��2����λ����ô�õ��������ߵĽ���ʽΪ ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com