
如图5317,以等腰直角△ABC两锐角顶点A,B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为( )

图5317
A.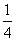 π B.
π B.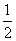 π C.
π C.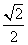 π D.
π D.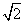 π
π
科目:初中数学 来源: 题型:
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.当同时转动两个转盘,停止后指针所指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段能构成三角形的概率为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
若用(1)、(2)、(3)、(4)四幅图分别表示变量之间的关系,将下面
的(a)、(b)、(c)、(d)对应的图象排序 ( )
 | |||||||
 | |||||||
 | |||||||
 |
(a)面积为定值的矩形(矩形的相邻两边长的关系)
(b)运动员推出去的铅球(铅球的高度与时间的关系)
(c)一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物质量的关系)
(d)某人从A地到B地后,停留一段时间,然后按原速返回(离开A地的距离与
时间的关系)
A.(3)(4)(1)(2) B.(3)(2)(1)(4)
C.(4)(3)(1)(2) D.(3)(4)(2)(1)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线 交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.

(1)请直接写出点C,D的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒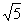 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
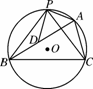
如图5125,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧 的中点,连接PA,PB,PC,PD.当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
的中点,连接PA,PB,PC,PD.当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
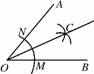
用直尺和圆规作一个角的平分线的示意图如图4218,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA C.AAS D.角平分线上的点到角两边的距离相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com