
科目:初中数学 来源: 题型:
| 2013 |
| x |
| 1 |
| 5 |
| 4 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:2013年湖南省长沙市高级中等学校招生考试数学 题型:044
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数y=![]() x2-
x2-![]() x-
x-![]() 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
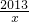 是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由; x2-
x2- x-
x- 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.查看答案和解析>>
科目:初中数学 来源:长沙 题型:解答题
| 2013 |
| x |
| 1 |
| 5 |
| 4 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:2013年湖南省长沙市中考数学试卷(解析版) 题型:解答题
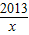 是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由; x2-
x2- x-
x- 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com