
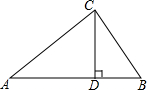
 如图所示,在△ABC中,CD⊥AB于点D,若AD=2BD,AC=4,BC=3,求BD的长.
如图所示,在△ABC中,CD⊥AB于点D,若AD=2BD,AC=4,BC=3,求BD的长.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
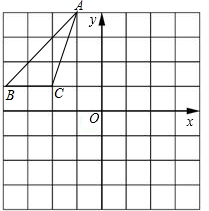 如图,在变长为1的小正方形组成的网格中,△ABC顶点均在格点上,且顶点坐标分别为A(-1,4),B(-4,1),C(-2,1);
如图,在变长为1的小正方形组成的网格中,△ABC顶点均在格点上,且顶点坐标分别为A(-1,4),B(-4,1),C(-2,1);查看答案和解析>>
科目:初中数学 来源: 题型:填空题
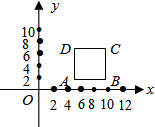 在如图所示的平面直角坐标系中有一边长为5的正方形,AB∥x轴,如果A点的坐标为(5,2),那么B点的坐标为(10,2),C点的坐标为(10,7),D点的坐标为5,7).
在如图所示的平面直角坐标系中有一边长为5的正方形,AB∥x轴,如果A点的坐标为(5,2),那么B点的坐标为(10,2),C点的坐标为(10,7),D点的坐标为5,7).查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
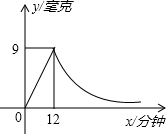 近来,禽流感又在抬头,已经夺去近10人的生命,病症与“非典”极为相似,为了同学们的身心健康,学校在休息日用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放过程中,y与x成反比例.如图所示,根据题中提供的信息,解答下列问题:
近来,禽流感又在抬头,已经夺去近10人的生命,病症与“非典”极为相似,为了同学们的身心健康,学校在休息日用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放过程中,y与x成反比例.如图所示,根据题中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
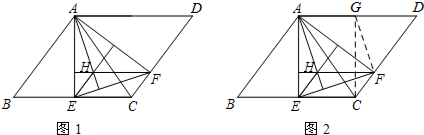
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com