
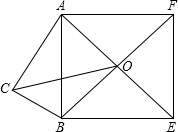
 如图,在Rt△ABC中,∠C=90°,AC=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,OC=4
如图,在Rt△ABC中,∠C=90°,AC=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,OC=4| 2 |
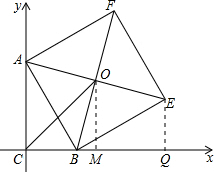 解:作EQ⊥x轴,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,3).
解:作EQ⊥x轴,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,3).
|
| 3+x |
| 2 |
| 1 |
| 2 |
| 3+x |
| 2 |
| 3+x |
| 2 |
| 3+x |
| 2 |
| 2 |
(
|


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com