
| A. | 1,2,2 | B. | 2,3,4 | C. | $\sqrt{2}$a,$\sqrt{3}$a,a | D. | 4,5,6 |
分析 分别把选项中的三边平方后,根据勾股定理逆定理即可判断能否构成直角三角形.
解答 解:A、∵12+22≠22,∴1,2,2不能构成直角三角形;
B、∵22+32≠42,∴2,3,4不能构成直角三角形;
C、∵($\sqrt{2}$a)2+a2=($\sqrt{3}$a)2,∴$\sqrt{2}$a,$\sqrt{3}$a,a能构成直角三角形;
D、∵42+52≠62,∴4,5,6不能构成直角三角形.
故选C.
点评 主要考查了利用勾股定理逆定理判定直角三角形的方法.在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
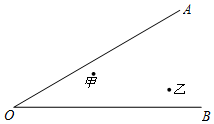 近年来,国家实施农村医疗卫生改革,某县计划在甲村、乙村之问设立一座定点医疗站点P,甲、乙两村坐落在两相交公路内(如图所示).医疗站必须适合下列条件:
近年来,国家实施农村医疗卫生改革,某县计划在甲村、乙村之问设立一座定点医疗站点P,甲、乙两村坐落在两相交公路内(如图所示).医疗站必须适合下列条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,若S1=4,S2=8,则AB的长为( )
如图,在Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,若S1=4,S2=8,则AB的长为( )| A. | 12 | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
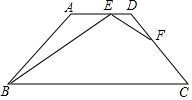 已知:如图,在梯形ABCD中,AD∥BC,AB=BC,AB=DC=AD=9,∠ABC=60°,点E,F分别在AD,DC上,且DE=3,CF=7.
已知:如图,在梯形ABCD中,AD∥BC,AB=BC,AB=DC=AD=9,∠ABC=60°,点E,F分别在AD,DC上,且DE=3,CF=7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com