练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点O(0，0)，A(0，1)是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA2A3B2，…，依此规律，则点A7的坐标是(　　)

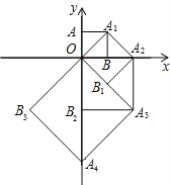
    A.(-8，0)B.(8，-8)C.(-8，8)D.(0，16)

    【答案】C

    【解析】

    根据正方形的性质，依次可求A2(2，0)，A3(2，2)，A4(0，-4)，A5(-4，-4)，A6(-8，0)，A7(-8，8)．

    解：∵O(0，0)，A(0，1)，

    ∴A1(1，1)，

    ∴正方形对角线OA1=，

    ∴OA2=2，

    ∴A2(2，0)，

    ∴A3(2，2)，

    ∴OA3=2，

    ∴OA4=4，

    ∴A4(0，-4)，A5(-4，-4)，A6(-8，0)，A7(-8，8)；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

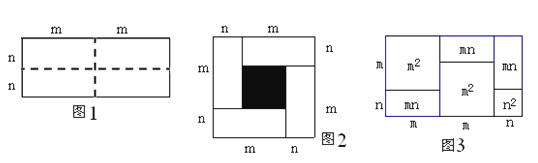
    【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形.

    (1)图2中的阴影部分的面积为 .

    (2)观察图2，请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.

    (3)根据你得到的关系式解答下列问题：若x+y=-6,xy=5,则x–y= .

    (4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

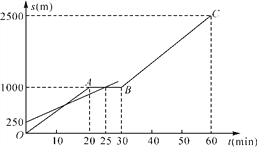
    【题目】小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500 m，如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象．

    (1)直接写出小明所走路程s与时间t的函数关系式；

    (2)小明出发多少时间与爸爸第三次相遇？

    (3)在速度都不变的情况下，小明希望比爸爸早20 min到达公园，则小明在步行过程中停留的时间需作怎样的调整？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

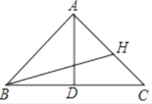
    【题目】如图，在△ABC中，AB＝10，BC＝12，BC边上的中线AD＝8．

    （1）证明：△ABC为等腰三角形；

    （2）点H在线段AC上，试求AH＋BH＋CH的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市大力发展绿色交通，构建公共绿色交通体系，“共享单车”的投入使用给人们的出行带来便利．小明随机调查了若干市民租用共享单车的骑车时间t（单位：分），将获得的数据分成四组，绘制了如图统计图，请根据图中信息，解答下列问题：

    （1）这次被调查的总人数是______；

    （2）补全条形统计图；

    （3）在扇形统计图中，求表示A组（t≤10分）的扇形圆心角的度数；

    （4）如果骑共享单车的平均速度为12km/h，请估算，在租用共享单车的市民中，骑车路程不超过6km的人数所占的百分比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数与一次函数y=kx+b的图象都经过点(-2，-1)，且当x=3时这两个函数值相等．

    (1)求这两个函数的解析式；

    (2)直接写出当x取何值时，成立．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

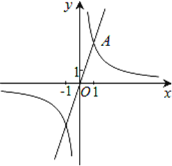
    【题目】如图，在平面直角坐标系xOy中，一次函数y=3x的图象与反比例函数的图象的一个交点为A（1，m）．

    （1）求反比例函数的解析式；

    （2）若点P在直线OA上，且满足PA=2OA，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

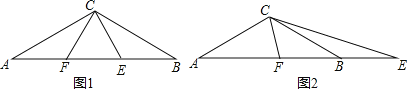
    【题目】如图1，△ABC中，CA＝CB，∠ACB＝120°，AB＝3，点E、F在直线AB上，且∠ECF＝60°．

    （1）求AC边的长；

    （2）如图1，点E、F在线段AB上时，若EF＝AF，求证：BE＝EF；

    （3）如图2，F在AB上，E在AB的延长线上时，AF＝m，BE＝n，则n＝　 　（用含m的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=x2﹣x﹣与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，点E（4，n）在抛物线上．

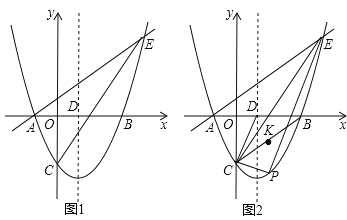
    （1）求直线AE的解析式；

    （2）点P为直线CE下方抛物线上的一点，连接PC，PE．当△PCE的面积最大时，连接CD，CB，点K是线段CB的中点，点M是CP上的一点，点N是CD上的一点，求KM+MN+NK的最小值；

    （3）点G是线段CE的中点，将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F．在新抛物线y′的对称轴上，是否存在一点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案