
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
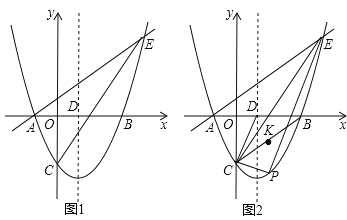
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+
x+![]() .(2)3,(3)点Q的坐标为(3,
.(2)3,(3)点Q的坐标为(3,![]() ),Q′(3,
),Q′(3,![]() )或(3,2
)或(3,2![]() )或(3,﹣
)或(3,﹣![]() ).
).
【解析】
试题分析:(1)抛物线的解析式可以变天为y=![]() (x+1)(x-3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入,求得k和b的值,从而得到AE的解析式;
(x+1)(x-3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入,求得k和b的值,从而得到AE的解析式;
(2)设直线CE的解析式为y=mx-![]() ,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE于点F,设点P的坐标为(x,
,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE于点F,设点P的坐标为(x,![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ),则点F(x,
),则点F(x,![]() x-
x-![]() ),则FP=﹣
),则FP=﹣![]() x2+
x2+![]() .由三角形的面积公式得:ΔEPC的面积=-
.由三角形的面积公式得:ΔEPC的面积=-![]() x2+
x2+![]() x,利用二次函数的媒体人富士康得x的值,从而求得点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP于N、M,然后利用轴对称的性质可得到点G和H的坐标,当点O、N、M、H在一条直线上时,KM+MN+NK有最小值,最小值=GH。
x,利用二次函数的媒体人富士康得x的值,从而求得点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP于N、M,然后利用轴对称的性质可得到点G和H的坐标,当点O、N、M、H在一条直线上时,KM+MN+NK有最小值,最小值=GH。
(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF、FQ=FQ三种情况求解即可.
试题解析:(1)∵y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ,
,
∴y=![]() (x+1)(x﹣3).
(x+1)(x﹣3).
∴A(﹣1,0),B(3,0).
当x=4时,y=![]() .
.
∴E(4,![]() ).
).
设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:
 ,
,
解得:k=![]() ,b=
,b=![]() .
.
∴直线AE的解析式为y=![]() x+
x+![]() .
.
(2)设直线CE的解析式为y=mx﹣![]() ,将点E的坐标代入得:4m﹣
,将点E的坐标代入得:4m﹣![]() =
=![]() ,解得:m=
,解得:m=![]() .
.
∴直线CE的解析式为y=![]() x﹣
x﹣![]() .
.
过点P作PF∥y轴,交CE与点F.
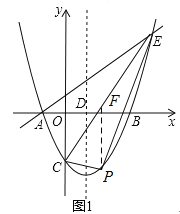
设点P的坐标为(x,![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ),则点F(x,
),则点F(x,![]() x﹣
x﹣![]() ),
),
则FP=(![]() x﹣
x﹣![]() )﹣(
)﹣(![]() x2﹣
x2﹣![]() x﹣
x﹣![]() )=
)=![]() x2+
x2+![]() x.
x.
∴△EPC的面积=![]() ×(
×(![]() x2+
x2+![]() x)×4=﹣
x)×4=﹣![]() x2+
x2+![]() x.
x.
∴当x=2时,△EPC的面积最大.
∴P(2,﹣![]() ).
).
如图2所示:作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.
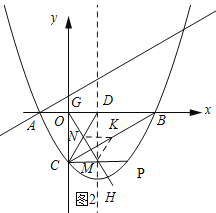
∵K是CB的中点,
∴k(![]() ,﹣
,﹣![]() ).
).
∵点H与点K关于CP对称,
∴点H的坐标为(![]() ,﹣
,﹣![]() ).
).
∵点G与点K关于CD对称,
∴点G(0,0).
∴KM+MN+NK=MH+MN+GN.
当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.
∴GH=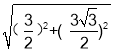 =3.
=3.
∴KM+MN+NK的最小值为3.
(3)如图3所示:

∵y′经过点D,y′的顶点为点F,
∴点F(3,﹣![]() ).
).
∵点G为CE的中点,
∴G(2,![]() ).
).
∴FG= .
.
∴当FG=FQ时,点Q(3,![]() ),Q′(3,
),Q′(3,![]() ).
).
当GF=GQ时,点F与点Q″关于y=![]() 对称,
对称,
∴点Q″(3,2![]() ).
).
当QG=QF时,设点Q1的坐标为(3,a).
由两点间的距离公式可知:a+![]() =
= ,解得:a=﹣
,解得:a=﹣![]() .
.
∴点Q1的坐标为(3,﹣![]() ).
).
综上所述,点Q的坐标为(3,![]() ),Q′(3,
),Q′(3,![]() )或(3,2
)或(3,2![]() )或(3,﹣
)或(3,﹣![]() ).
).


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
一次函数与方程的关系:
①一次函数的解析式就是一个二元一次方程;
②点B的横坐标是方程①的解;
③点C的坐标(x,y)中的x,y的值是方程组②的解
一次函数与不等式的关系:
①函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式③的解集;
②函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式④的解集.
(1)请根据以上方框中的内容在下面数学序号后写出相应的式子:
①;②;③;④;
(2)如果点C的坐标为(2,5),那么不等式kx+b≥k1x+b1的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观测信息如下:

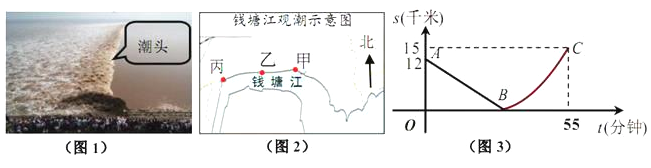
按上述信息,小红将“交叉潮”形成后潮头与乙地质检的距离![]() (千米)与时间
(千米)与时间![]() (分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点![]() ,点
,点![]() 坐标为
坐标为![]() ,曲线
,曲线![]() 可用二次函数:s=
可用二次函数:s=![]() ,(
,(![]() 是常数)刻画.
是常数)刻画.
(1)求![]() 值,并求出潮头从甲地到乙地的速度;
值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以![]() 千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为![]() 千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度![]() ,
,![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
已知:如图, ![]() 及AC边的中点O,
及AC边的中点O,
求作:平行四边形ABCD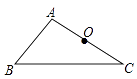
小敏的作法如下:
① 连接BO并延长,在延长线上截取OD=BO
② 连接DA、DC,
所以四边形ABCD就是所求作的平行四边形。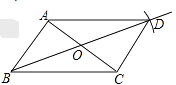
老师说:”小敏的作法正确.“
请回答:小敏的作法正确的理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=2x﹣2与x轴交于点A,与y轴交于点B.
(1)求点A、B的坐标;
(2)点C在x轴上,且S△ABC=3S△AOB , 直接写出点C坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.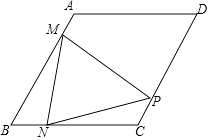
(1)当t=2时,∠NMP=度;
(2)求t为何值时,以A、M、C、P为顶点的四边形是平行四边形;
(3)当△NPC为直角三角形时,求此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校初四年纪学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
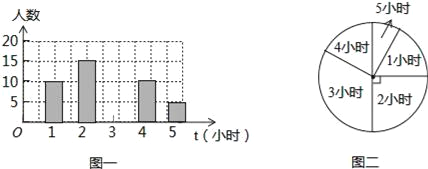
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com