
【题目】为了了解某学校初四年纪学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
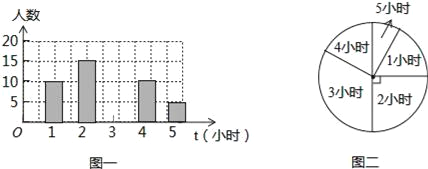
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
【答案】(1)①m=60;②30o;③见解析;(2)众数、中位数为5;平均数2.92.
【解析】试题分析:(1)①根据2小时所占扇形的圆心角的度数确定其所占的百分比,然后根据条形统计图中2小时的人数求得m的值;
②结合周角是360度进行计算;
③求得总人数后减去其他小组的人数即可求得第三小组的人数;
(2)利用众数、中位数的定义及平均数的计算公式确定即可.
试题解析:
(1)①∵课外阅读时间为2小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为![]() ,
,
∵课外阅读时间为2小时的有15人,
∴m=15÷![]() =60;
=60;
②5小时的扇形圆心角的度数: ![]() ,
,
③第三小组的频数为:60-10-15-10-5=20,
补全条形统计图为:
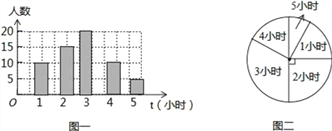
(2)∵课外阅读时间为3小时的20人,最多,
∴众数为 3小时;
∵共60人,中位数应该是第30和第31人的平均数,且第30和第31人阅读时间均为3小时,
∴中位数为3小时;平均数为: ![]() ≈2.92小时.
≈2.92小时.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
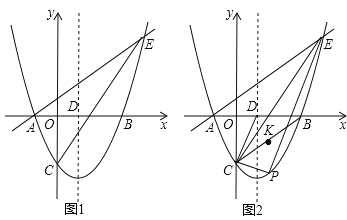
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
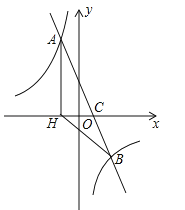
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n)
,点B的坐标为(4,n)
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深高北校区初二年级举行“名著知识竟赛”决赛.在这之前,初二(24)班举行了三轮初赛,为了从甲乙两名平均分最高的同学中选取一名发挥稳定的同学参加决赛,需要考察这两位同学三轮初赛成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为 . 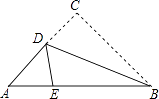
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋小长假首日,好天气给了游客好心情.9月22日,现代快报记者从南京市旅游委获悉,截至当天下午4点,南京七大景区总接待量364000人次.将364000人次用科学记数法表示为______人次.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com