
����Ŀ��С����ѧϰ��һ�η��̣��飩��һԪһ�β���ʽ��һ�κ��������֪ʶ�����������£�
һ�κ����뷽�̵Ĺ�ϵ��
��һ�κ����Ľ���ʽ����һ����Ԫһ�η��̣�
�ڵ�B�ĺ������Ƿ������Ľ⣻
�۵�C�����꣨x��y���е�x��y��ֵ�Ƿ��������Ľ�
һ�κ����벻��ʽ�Ĺ�ϵ��
�ٺ���y=kx+b�ĺ���ֵyС��0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ���Ľ⼯��
�ں���y=kx+b�ĺ���ֵy����0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ���Ľ⼯��
��1����������Ϸ����е�������������ѧ��ź�д����Ӧ��ʽ�ӣ�
����������������
��2�������C������Ϊ��2��5������ô����ʽkx+b��k1x+b1�Ľ⼯�� ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+b������A����30��0���͵�B��0��15����ֱ��y=x+5��ֱ��y=kx+b�ཻ�ڵ�P����y�ύ�ڵ�C��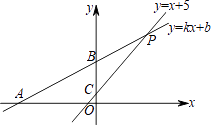
��1����ֱ��y=kx+b�Ľ���ʽ��
��2�����PBC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A. �����ȵ�����������ȫ�� B. ȫ�������ζ�Ӧ���ϵ��������
C. ȫ�������εĶ�Ӧ�ǵĽ�ƽ������� D. ȫ�������εĶ�Ӧ���ϵĸ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
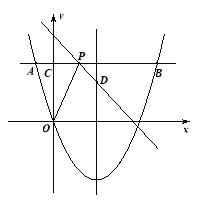
����Ŀ��������10�֣���ͼ����������![]() ��һ��A��
��һ��A��![]() ���ƽ���ߣ�������������һ��B����
���ƽ���ߣ�������������һ��B����![]() ���ڵ�C����֪��A�ĺ�����Ϊ
���ڵ�C����֪��A�ĺ�����Ϊ![]() ��
��
��1���������ߵĶԳ���͵�B�����ꣻ
��2����AB����ȡһ��P������OP������C����ֱ��OP�ĶԳƵ�D��
������BD����BD����Сֵ��
������D���������ߵĶԳ����ϣ�����![]() ���Ϸ�ʱ����ֱ��PD�ĺ�������ʽ��
���Ϸ�ʱ����ֱ��PD�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ���ƽ���ı��������ֱ�߳�Ϊ�����ߡ��������������ͼ�����Եõ��ı��εġ����ߡ�����ͼ1�ı���ABCD�У�ȡ�Խ���BD���е�O������OA��OC����Ȼ������AOC��ƽ���ı���ABCD��������ٹ���O��OE��AC��CD��E����ֱ��AE��Ϊһ�������ߡ���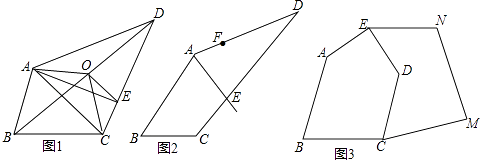
��1����ͼ1����˵��ֱ��AE�ǡ����ߡ������ɣ�
��2����ͼ2��AEΪһ�������ߡ���FΪAD���ϵ�һ�㣬����������F��ġ����ߡ�����˵�����ɣ�
��3����ͼ3�������ABCDE��һ�����ص�ʾ��ͼ���������꿪�ѻĵأ����ѱ����ͼ3��ʾ����״����ԭ�������뿪�ѻĵصķֽ�С·������CDE���������ţ����������E����һ��ֱ·��Ҫ��ֱ·��ߵ����������ԭ��һ���ֻࣨ�����ͼ�ʵ�˵������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڼ���һ������ʽ��ƽ��ʱ���õ���ȷ���m2��10mn+���������һ�����īˮ��Ⱦ����һ��Ӧ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=![]() x2��
x2��![]() x��
x��![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
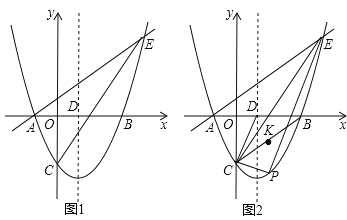
��1����ֱ��AE�Ľ���ʽ��
��2����PΪֱ��CE�·��������ϵ�һ�㣬����PC��PE������PCE��������ʱ������CD��CB����K���߶�CB���е㣬��M��CP�ϵ�һ�㣬��N��CD�ϵ�һ�㣬��KM+MN+NK����Сֵ��
��3����G���߶�CE���е㣬��������y=![]() x2��
x2��![]() x��
x��![]() ��x��������ƽ�Ƶõ���������y�䣬y�侭����D��y��Ķ���Ϊ��F������������y��ĶԳ����ϣ��Ƿ����һ��Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��x��������ƽ�Ƶõ���������y�䣬y�侭����D��y��Ķ���Ϊ��F������������y��ĶԳ����ϣ��Ƿ����һ��Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
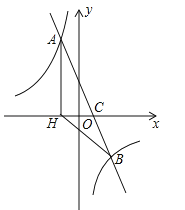
����Ŀ����ͼ����ƽ��ֱ������ϵ����һ�κ���y=ax+b��a��0����ͼ���뷴��������![]() ��k��0����ͼ����A��B��������x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е���AC=
��k��0����ͼ����A��B��������x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е���AC=![]() ��cos��ACH=
��cos��ACH=![]() ����B��������4��n��
����B��������4��n��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������BCH�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com